Angle between two straight lines

Angle between two straight lines

(a) Vector form

The acute angle between two given straight lines

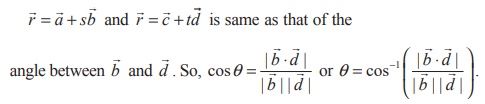
(b) Cartesian form

If two lines are given in Cartesian form as 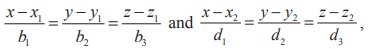 then the acute angle θ between the two given lines is given by

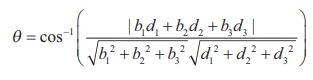
Remark

(i) The two given lines with direction ratios b1 , b2 , b3 and d1 , d2 , d3 are parallel if, and only if .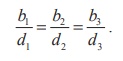

(ii)  The two given lines with direction ratios b1, b2, b3 and d1, d2, d3 are perpendicular if and only if b1d1 + b2d2 + b3d3 = 0 .

(iii) If the direction cosines of two given straight lines are l1 , m1 , n1 and l2 , m2 , n2, then the angle between the two given straight lines is cos θ =| l1l2 + m1m2 + n1n2 | .

Example 6.29

Find the acute angle between the lines  = (ˆi + 2ˆj + 4ˆk ) + t(2ˆi + 2ˆj + Ë†k ) and the straight line passing through the points (5,1, 4) and (9, 2,12) .

Solution

We know that the line  = (ˆi + 2ˆj + 4ˆk ) + t(2ˆi + 2ˆj + Ë†k ) is parallel to the vector 2ˆi + 2ˆj + Ë†k.

Direction ratios of the straight line joining the two given points (5,1, 4) and (9, 2,12) are 4,1,8 and hence this line is parallel to the vector 4iˆ + ˆj + 8kˆ .

Therefore, the acute angle between the given two straight lines is

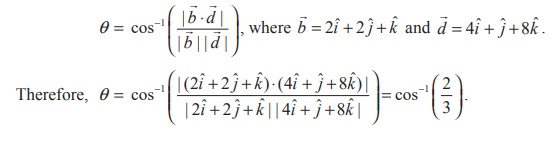
Example 6.30

Find the acute angle between the straight lines  and state whether they are parallel or perpendicular.

Solution

Comparing the given lines with the general Cartesian equations of straight lines,

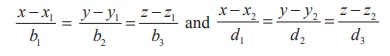
we find (b1 , b2 , b3 ) = (2,1, −2) and (d1 , d2 , d3 ) = (4, −4, 2) . Therefore, the acute angle between the two straight lines is

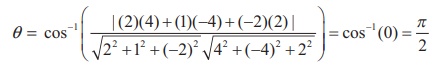
Thus the two straight lines are perpendicular.

Example 6.31

Show that the straight line passing through the points A(6, 7, 5) and B(8,10, 6) is perpendicular to the straight line passing through the points C(10, 2, −5) and D(8, 3, −4) .

Solution

The straight line passing through the points A(6, 7, 5)  and B(8,10, 6) is parallel to the vector  =  =  âˆ’  = 2iˆ + 3 ˆj + kˆ and the straight line passing through the points C(10, 2, −5) and D(8, 3, −4) is parallel to the vector  =  = −2iˆ + ˆj + kˆ . Therefore, the angle between the two straight lines is the angle between the two vectors  and . Since

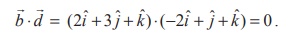
the two vectors are perpendicular, and hence the two straight lines are perpendicular.

Aliter

We find that direction ratios of the straight line joining the points A(6, 7, 5) and B(8,10, 6) are (b1 , b2 , b3 ) = (2, 3,1) and and direction ratios of the line joining the points C(10, 2, −5) and D(8, 3, −4) are (d1 , d2 , d3 ) = (−2,1,1) . Since b1d1 + b2d2 + b3d3 = (2)(−2) + (3)(1) + (1)(1) = 0 , the two straight lines are perpendicular.

Example 6.32

Show that the lines 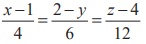 and 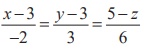  are parallel

Solution

We observe that the straight line 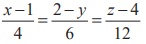 is parallel to the vector 4iˆ - 6 ˆj +12kˆ and the straight line  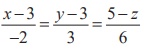is parallel to the vector -2iˆ + 3ˆj - 6kˆ.

Since 4iˆ - 6ˆj +12kˆ = -2(-2iˆ + 3ˆj - 6kˆ) , the two vectors are parallel, and hence the two straight lines are parallel.