Exercise 6.2: Scalar triple product

EXERCISE 6.2

1. 

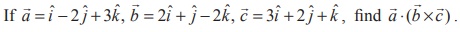
2. Find the volume of the parallelepiped whose coterminous edges are represented by the vectors -6iˆ +14ˆj +10kˆ, 14iˆ - 10ˆj - 6kˆ and 2iˆ + 4 Ë†j - 2kˆ .

3. The volume of the parallelepiped whose coterminus edges are 7iˆ + Î» Ë†j âˆ’ 3kˆ, iˆ + 2 Ë†j âˆ’ kˆ, âˆ’3iˆ + 7 Ë†j + 5kˆ is 90 cubic units. Find the value of Î» .

4. If ,,  are three non-coplanar vectors represented by concurrent edges of a parallelepiped of volume 4 cubic units, find the value of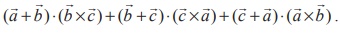 

5. Find the altitude of a parallelepiped determined by the vectors  = âˆ’2i + 5 j + 3k,  = i + 3 j âˆ’ 2k  and   = -3i + j âˆ’ 2k  if the base is taken as the parallelogram determined by and .

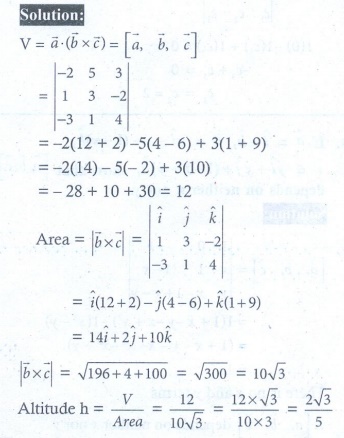
6. Determine whether the three vectors 2iˆ + 3 Ë†j + kˆ, iˆ âˆ’ 2 Ë†j + 2kˆ and 3iˆ + Ë†j + 3kˆ are coplanar.

7. Let  = Ë†i + Ë†j + Ë†k,  = i and c = c1ˆi + c2 Ë†j + c3ˆk . If c1 = 1 and c2 = 2 , find c3 such that , and  are coplanar.

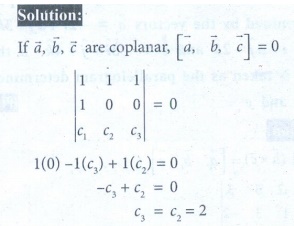
8. If 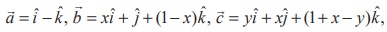 show that [, , ] depends on neither x nor y .

9. If the vectors are aiˆ + a Ë†j + akˆ , iˆ + kˆ  and ciˆ + c Ë†j + bkˆ  are coplanar, prove that c is the geometric  mean of a and b .

10. Let ,,  be three non-zero vectors such that  is a unit vector perpendicular to both and  . If the angle between  and  is Ï€/6. Show that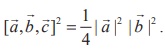 

Answers:

1. 24

2. 720 cubic units

3. −5

4. ±12

5. 2√3 / 5

6. coplanar

7. 2