Chapter: 12th Mathematics : UNIT 6 : Applications of Vector Algebra
Equation of a plane passing through a given point and parallel to two given non-parallel vectors
Equation
of a plane passing through a given point and parallel to two given non-parallel
vectors.
(a) Parametric form of vector equation
Consider a plane passing through a given point A with
position vector 
and parallel to two given non-parallel vectors 
and 
. If 
is the position
vector of an arbitrary point P on the plane, then the vectors and are coplanar. So, ( − )
lies in the plane containing and .
Then, there exists scalars s, t ∈ R such that 
which implies
, where s, t ∈ R ... (1)
This is the parametric form of vector equation of the plane
passing through a given point and parallel to two given non-parallel vectors .
(b) Non-parametric form of vector equation
Equation (1) can be equivalently written as
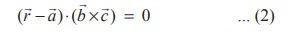
which is the non-parametric form of vector equation of the plane
passing through a given point and parallel to two given non-parallel vectors .
(c) Cartesian form of equation
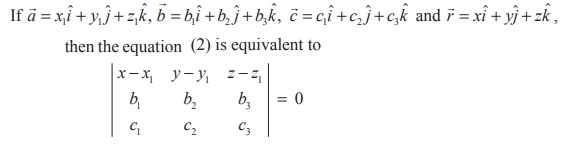
This is the Cartesian equation of the plane passing through a
given point and parallel to two given non-parallel vectors.
Related Topics