Definition, Theorem, Proof, Solved Example Problems, Solution - Angle between two planes | 12th Mathematics : UNIT 6 : Applications of Vector Algebra
Chapter: 12th Mathematics : UNIT 6 : Applications of Vector Algebra
Angle between two planes
Angle
between two planes
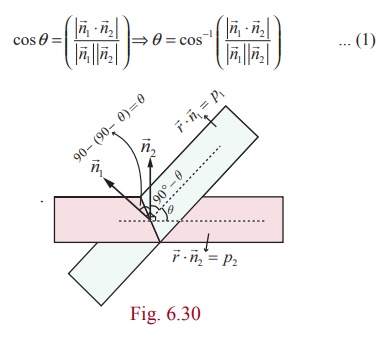
The angle between two given planes is same as the angle between
their normals.
Proof
If θ is the acute angle between two planes ![]() ⋅
⋅ ![]() 1 = p1 and
1 = p1 and ![]() ⋅
⋅![]() 2 = p2 , then θ is the acute angle between their
normal vectors
2 = p2 , then θ is the acute angle between their
normal vectors ![]() 1 and
1 and ![]() 2
2
Therefore,
Remark
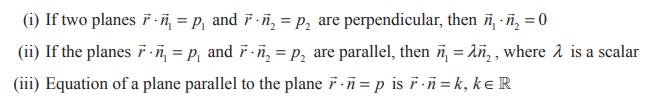
Theorem 6.19
The acute angle θ between the planes a1x
+ b1y + c1z + d1
= 0 and

Proof
If ![]() 1 and
1 and ![]() 2 are the vectors normal to the two
given planes a1x + b1y + c1z + d1 = 0 and a2x + b2y + c2z + d2
= 0 respectively. Then,
2 are the vectors normal to the two
given planes a1x + b1y + c1z + d1 = 0 and a2x + b2y + c2z + d2
= 0 respectively. Then, 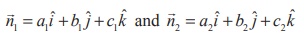
Therefore, using equation (1) in theorem 6.18 the acute angle θ
between the planes is given by
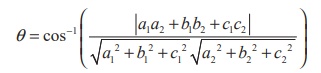
Remark
(i) The planes a1x + b1y + c1z +
d1 = 0 and a2x + b2y + c2z + d2
= 0 are perpendicular if a1a2 + b1b2 + c1c2 = 0
(ii) The planes a1x + b1 y + c1z
+ d1 = 0 and a2x + b2y + c2z + d2
= 0 are parallel if 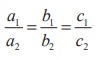
(iii) Equation of a plane parallel to the plane ax + by + cz = p is ax + by + cz = k , k ∈ R.
Example 6.47
Find the acute angle between the planes ![]() .(2 ˆi + 2ˆ j + 2ˆk ) = 11 and 4x - 2 y + 2z = 15
.(2 ˆi + 2ˆ j + 2ˆk ) = 11 and 4x - 2 y + 2z = 15
Solution
The normal vectors of the two given planes ![]() = (2 ˆi + 2ˆ j + 2ˆk ) = 11 and 4x - 2
y + 2z = 15 are
= (2 ˆi + 2ˆ j + 2ˆk ) = 11 and 4x - 2
y + 2z = 15 are ![]() 1 = 2ˆi
+ 2ˆ j + 2ˆk and
1 = 2ˆi
+ 2ˆ j + 2ˆk and ![]() 2 = 4ˆi - 2ˆ j + 2ˆk respectively.
2 = 4ˆi - 2ˆ j + 2ˆk respectively.
If θ is the acute angle between the planes, then we have
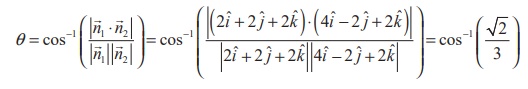
Related Topics
