Chapter: 12th Mathematics : UNIT 6 : Applications of Vector Algebra
Equation of line of intersection of two planes
Equation
of line of intersection of two planes
Let ![]() ⋅
⋅![]() = p and
= p and ![]() ⋅
⋅![]() = q be two non-parallel
planes. We know that
= q be two non-parallel
planes. We know that ![]() and
and ![]() are perpendicular
to the given planes respectively.
are perpendicular
to the given planes respectively.
So, the line of intersection of these planes is
perpendicular to both ![]() ×
× ![]() .
. ![]() and
and ![]() .
Therefore, it is parallel to the vector
.
Therefore, it is parallel to the vector ![]() ×
× ![]() . Let
. Let
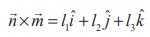

Consider the equations of two planes a1x + b1y + c1z = p and a2x + b2y + c2z = q . The line of intersection of the two given planes intersects atleast one of the coordinate planes. For simplicity, we assume that the line meets the coordinate plane z = 0 . Substitute z=0 and obtain the two equations a1x + b1y − p = 0 and a2 x + b2y − q = 0 .Then by solving these equations, we get the values of x and y as x1 and y1 respectively.
So, ( x1 , y1 , 0) is
a point on the required line, which is parallel to l1iˆ
+ l2 ˆj + l3kˆ . So, the
equation of the line is
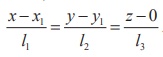
Related Topics