Equation of a plane when a normal to the plane

Equation of a plane when a normal to the plane and the distance of the plane from the origin are given

(a) Vector equation of a plane in normal form

Theorem 6.15

The equation of the plane at a distance p from the origin and perpendicular to the unit normal vector dˆ is â‹… dˆ = p .

Proof

Consider a plane whose perpendicular distance from the origin is p . 

Let A be the foot of the perpendicular from to the plane. 

Let dˆ be the unit normal vector in the direction of .

Then  = pdˆ .

If  is the position vector of an arbitrary point P on the plane,

then  is perpendicular to .

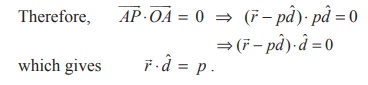
The above equation is called the vector equation of the plane in normal form.

(b) Cartesian equation of a plane in normal form

Let l, m, n be the direction cosines of dˆ. Then we have dˆ = liˆ + mˆj + nkˆ.

Thus, equation (1) becomes

 . (liˆ + mˆj + nkˆ) = p

If P is (x,y,z), then  = xˆi + yˆj + zˆk

Therefore, (xiˆ + yˆj + zkˆ) â‹… (liˆ + mˆj + nkˆ) = p or lx + my + nz = p                     ............(2)

Equation (2) is called the Cartesian equation of the plane in normal form.

Remark

(i) If the plane passes through the origin, then p = 0 . So, the equation of the plane is lx + my + nz = 0.

 (ii) If  is normal vector to the plane, then Ë†d =  is a unit normal to the plane. So, the vector equation of the plane is .  = p or  .  = q , where q = p |  | . The equation  .  = q is the vector equation of a plane in standard form.

Note

In the standard form   .   = q ,   need not be a unit normal and q need not be the perpendicular distance.