Definition, Theorem, Proof - Equation of a plane passing through three given non-collinear points | 12th Mathematics : UNIT 6 : Applications of Vector Algebra
Chapter: 12th Mathematics : UNIT 6 : Applications of Vector Algebra
Equation of a plane passing through three given non-collinear points
Equation
of a plane passing through three given non-collinear points
(a) Parametric form of vector equation
Theorem 6.17
If three non-collinear points with position vectors 
, 
, 
are
given, then the vector equation of the plane passing through the given points
in parametric form is
Proof
Consider a plane passing through three non-collinear points A,
B, C with position vectors , , respectively.
Then atleast two of them are non-zero vectors. Let us take ≠0 and ≠0 . Let 
be the position vector of an arbitrary point P on the
plane. Take a point D on AB (produced) such that 
is
parallel to 
and 
is parallel to 
. Therefore,
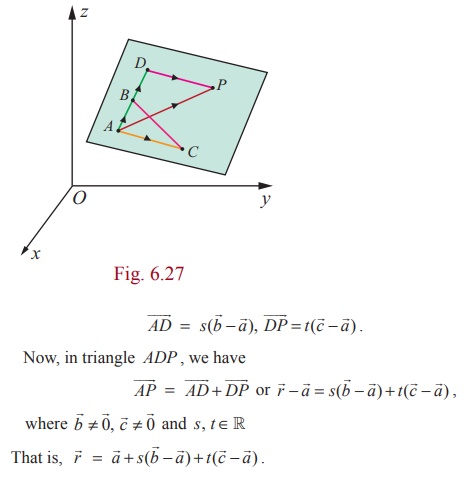
This is the parametric form of vector equation of the plane
passing through the given three non-collinear points.
(b) Non-parametric form of vector equation
Let A, B, and C be the three non collinear
points on the plane with position vectors , , respectively. Then atleast two of them are
non-zero vectors. Let us take ≠0 and ≠0 .
Now = - and = - . The
vectors ( - and - lie on the
plane. Since , , are non-collinear, is not parallel to .
Therefore,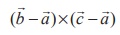 
is perpendicular
to the plane.
If is the position vector of an arbitrary point
P(x, y, z)
on the plane, then the equation of the plane passing through the point A with
position vector and perpendicular to the vector 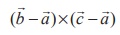is given
by
This is the non-parametric form of vector equation of the plane
passing through three non-collinear points.
(c) Cartesian form of equation
If (x1 , y1 , z1
), (x2 , y2 , z2 ) and (x3
, y3 , z3 ) are the coordinates of three
non-collinear points A, B, C with position vectors , , respectively and (x, y, z) is
the coordinates of the point P with position vector , then we have
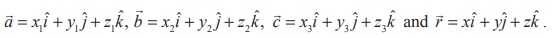
Using these vectors, the non-parametric form of vector equation
of the plane passing through the given three non-collinear points can be
equivalently written as
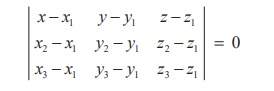
which is the Cartesian equation of the plane passing through
three non-collinear points.
Related Topics