Chapter: 12th Mathematics : UNIT 6 : Applications of Vector Algebra
Geometric introduction to vectors
Geometric
introduction to vectors
A vector ![]() is represented as a
directed straight line segment in a 3-dimensional space R3 , with an
initial point A = (a1, a2, a3) ∈ R3 and an end point B
= (b1,
b2, b3 )∈ R3 , and it is
denoted by
is represented as a
directed straight line segment in a 3-dimensional space R3 , with an
initial point A = (a1, a2, a3) ∈ R3 and an end point B
= (b1,
b2, b3 )∈ R3 , and it is
denoted by ![]() . The length of the line segment AB
is the magnitude of the vector
. The length of the line segment AB
is the magnitude of the vector ![]() and the direction from A
to B is the direction of the vector
and the direction from A
to B is the direction of the vector ![]() . Hereafter,
a vector will be interchangeably denoted by
. Hereafter,
a vector will be interchangeably denoted by ![]() or
or ![]() . Two vectors
. Two vectors ![]() and
and ![]() in R3 are said to be equal if
and only if the length AB is equal to the length CD and the
direction from A to B is parallel to the direction from C to
D . If
in R3 are said to be equal if
and only if the length AB is equal to the length CD and the
direction from A to B is parallel to the direction from C to
D . If ![]() and
and ![]() are equal, we write
are equal, we write ![]() =
= ![]() , and
, and ![]() is called a translate of
is called a translate of ![]() .
.
It is easy to observe that every vector ![]() can be
translated to anywhere in R3
, equal to a vector with initial point U ∈ R3 and end point V ∈ R 3 such that
can be
translated to anywhere in R3
, equal to a vector with initial point U ∈ R3 and end point V ∈ R 3 such that ![]() =
= ![]() . In
particular, if O is the origin of R3 , then a point P ∈ R3 can
be found such that
. In
particular, if O is the origin of R3 , then a point P ∈ R3 can
be found such that ![]() =
= ![]() . The vector
. The vector ![]() is called the position vector of the point P . Moreover, we observe
that given any vector
is called the position vector of the point P . Moreover, we observe
that given any vector ![]() , there exists a unique point P ∈ R3 such that the
position vector
, there exists a unique point P ∈ R3 such that the
position vector ![]() of P is equal to
of P is equal to ![]() .
A vector
.
A vector ![]() is said to be the zero vector if the initial point A
is the same as the end point B . We use the standard notations iˆ,
ˆj, kˆ and
is said to be the zero vector if the initial point A
is the same as the end point B . We use the standard notations iˆ,
ˆj, kˆ and ![]() to denote the position vectors of the points
(1, 0, 0),(0,1, 0),(0, 0,1), and (0, 0, 0), respectively. For a given point (a1, a2, a3)
∈ R3, aiˆ + a ˆj + akˆ
is called the position vector of the point (a1, a2,
a3) which is the directed
straight line segment with initial point (0, 0, 0) and end point (a1
, a2 , a3 ) . All real numbers are called
scalars.
to denote the position vectors of the points
(1, 0, 0),(0,1, 0),(0, 0,1), and (0, 0, 0), respectively. For a given point (a1, a2, a3)
∈ R3, aiˆ + a ˆj + akˆ
is called the position vector of the point (a1, a2,
a3) which is the directed
straight line segment with initial point (0, 0, 0) and end point (a1
, a2 , a3 ) . All real numbers are called
scalars.
Given a vector ![]() , the length of the vector
|
, the length of the vector
|![]() | is
calculated by
| is
calculated by
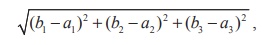
where A is (a1 , a2 ,
a3 ) and B is (b1 , b2
, b3 ). In particular, if a vector is the position vector ![]() of (b1 , b2 , b3 ),
then its length is
of (b1 , b2 , b3 ),
then its length is
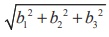
A vector having length 1 is called a unit vector. We the notation uˆ
, for a unit vector. Note that iˆ, ˆj , and kˆ use
are unit vectors and ![]() is the unique vector with length 0 . The
direction of
is the unique vector with length 0 . The
direction of ![]() is specified according to the context.
is specified according to the context.
The addition and scalar multiplication on vectors in 3-dimensional space are defined
by
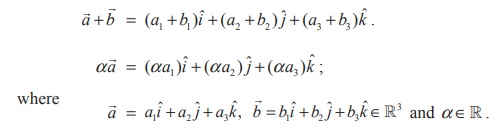
To see the geometric interpretation of ![]() +
+ ![]() ,
let
,
let ![]() and
and ![]() , denote the position vectors of A =
(a1 , a2 , a3 ) and B =
(b1 , b2 , b3 ) ,
respectively. Translate the position vector
, denote the position vectors of A =
(a1 , a2 , a3 ) and B =
(b1 , b2 , b3 ) ,
respectively. Translate the position vector ![]() to the vector
with initial point as A and end point as C = (c1
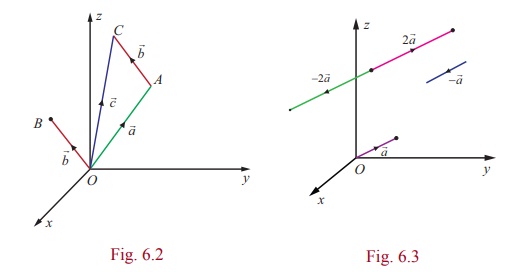
, c2 , c3 ) , for a suitable (c1 , c2 , c3 ) ∈ R3. See the Fig (6.2). Then, the position vector
to the vector
with initial point as A and end point as C = (c1
, c2 , c3 ) , for a suitable (c1 , c2 , c3 ) ∈ R3. See the Fig (6.2). Then, the position vector ![]() of the point (c1 , c2 , c3
) is equal to
of the point (c1 , c2 , c3
) is equal to ![]() +
+ ![]() .
.
The vector α![]() is another vector parallel to
is another vector parallel to ![]() and
its length is magnified (if α > 1) or contracted (if 0 < α
< 1) . If α < 0 , then α
and
its length is magnified (if α > 1) or contracted (if 0 < α
< 1) . If α < 0 , then α ![]() is a vector
whose magnitude is | α | times that of
is a vector
whose magnitude is | α | times that of ![]() and
direction opposite to that of
and
direction opposite to that of ![]() . In particular, if α =
−1, then α
. In particular, if α =
−1, then α![]() = −
= −![]() is the vector with same length
and direction opposite to
that of
is the vector with same length
and direction opposite to
that of ![]() . See Fig. 6.3
. See Fig. 6.3
Related Topics