Definition, Theorem, Proof, Solved Example Problems, Solution - Shortest distance between two straight lines | 12th Mathematics : UNIT 6 : Applications of Vector Algebra
Chapter: 12th Mathematics : UNIT 6 : Applications of Vector Algebra
Shortest distance between two straight lines
Shortest distance between two straight lines
We have just explained how the point of intersection of two lines
are found and we have also studied how to determine whether the given two lines
are parallel or not.
Definition 6.6
Two lines are said to be coplanar if they lie in the same plane.
Note
If two lines are either parallel or intersecting, then they are
coplanar.
Definition 6.7
Two lines in space are called skew lines if they are not parallel and do not intersect
Note
If two lines are skew lines, then they are non coplanar. If the
lines are not parallel and intersect, the distance between them is zero. If
they are parallel and non-intersecting, the distance is determined by the
length of the line segment perpendicular to both the parallel lines. In the
same way, the shortest distance between two skew lines is defined as the length
of the line segment perpendicular to both the skew lines. Two lines will either
be parallel or skew.
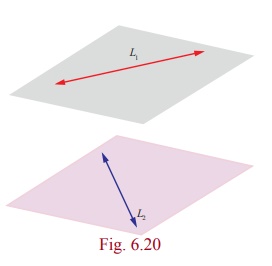

Proof
The given two parallel lines ![]() =
= ![]() + s
+ s![]() and
and ![]() =
= ![]() + t
+ t![]() are denoted
by L1 and L2 respectively. Let A and
B be the points on L1 and L2 whose
position vectors are
are denoted
by L1 and L2 respectively. Let A and
B be the points on L1 and L2 whose
position vectors are ![]() and
and ![]() respectively. The two
given lines are parallel to
respectively. The two
given lines are parallel to ![]() .
.
Let AD be a perpendicular to the two given lines. If θ is
the acute angle between ![]() and
and ![]() , then
, then

But, from the right angle triangle ABD ,
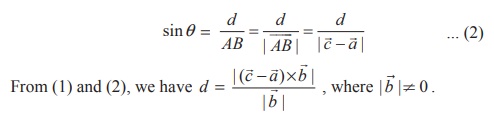

Proof
The two skew lines ![]() =
= ![]() + s
+ s![]() and
and ![]() =
= ![]() + t
+ t![]() are denoted by L1
and L2 respectively.
are denoted by L1
and L2 respectively.
Let A and C be the points on L1
and L2 with position vectors ![]() and
and ![]() respectively.
respectively.
From the given equations of skew lines, we observe that L1
is parallel to the vector ![]() and L2 is parallel
to the vector
and L2 is parallel
to the vector ![]() . So,
. So, ![]() ×
× ![]() is perpendicular
to the lines L1 and L2.
is perpendicular
to the lines L1 and L2.
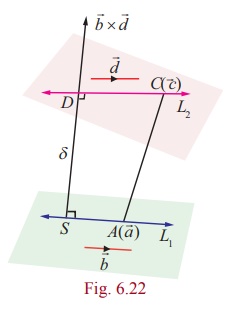
Let SD be the line segment perpendicular to both the
lines L1 and L2. Then the vector ![]() is perpendicular to the vectors
is perpendicular to the vectors ![]() and
and ![]() and therefore it is
parallel to the vector
and therefore it is
parallel to the vector ![]() ×
× ![]() .
.
So, 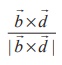 is a unit vector in the direction of
is a unit vector in the direction of ![]() . Then, the shortest distance |
. Then, the shortest distance | ![]() | is the absolute value of the
projection of
| is the absolute value of the
projection of ![]() on
on ![]() . That is,
. That is,
δ = | ![]() | =|
| =| ![]() . (Unit vector in the direction of
. (Unit vector in the direction of ![]() )|
)|
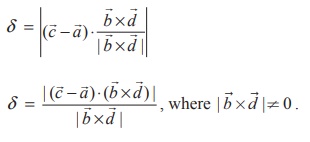
Remark
(i) It follows from theorem (6.14) that two straight lines ![]() =
=
![]() + s
+ s![]() and
and ![]() =
= ![]() + t
+ t![]() intersect
each other (that is, coplanar) if (
intersect
each other (that is, coplanar) if (![]() -
- ![]() ) . (
) . (![]() ×
×![]() ) = 0
) = 0
(2) If two
lines 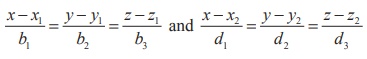 intersect each other (that is, coplanar), then we have
intersect each other (that is, coplanar), then we have
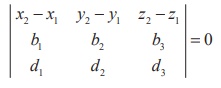
Example 6.34
Find the parametric form of vector equation of a straight line
passing through the point of intersection of the straight lines 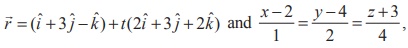 and perpendicular to both straight lines.
and perpendicular to both straight lines.
Solution
The Cartesian equations of the straight line ![]() =
(iˆ + 3 ˆj − k ) + t(2iˆ + 3 ˆj + 2k
) is
=
(iˆ + 3 ˆj − k ) + t(2iˆ + 3 ˆj + 2k
) is
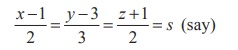
Then any point on this line is of the form (2s +1, 3s + 3, 2s -1) ... (1)
The Cartesian equation of the second line is (x – 2)/1 = (y – 4)/2 = (z
+ 3)/4 = t (say)
Then any point on this line is of the form (t + 2, 2t + 4, 4t - 3)
If the given lines intersect, then there must be a common point.
Therefore, for some s, t ∈ R, we have (2s +1, 3s + 3, 2s −1)
= (t + 2, 2t + 4, 4t − 3) .
Equating the coordinates of x, y and z we
get
2s − t = 1, 3s − 2t = 1 and s −
2t = −1.
Solving the first two of the above three equations, we get s =
1 and t = 1. These values of s and t satisfy the third
equation. So, the lines are intersecting.
Now, using the value of s in (1) or the value of t in
(2), the point of intersection (3, 6,1) of these two straight lines is
obtained.
If we take ![]() = 2iˆ
+ 3ˆj + 2kˆ and
= 2iˆ
+ 3ˆj + 2kˆ and ![]() = iˆ + 2ˆj + 4kˆ then
= iˆ + 2ˆj + 4kˆ then 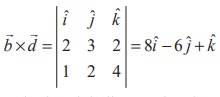 is a vector perpendicular to both the given straight lines.
Therefore, the required straight line passing through (3, 6,1) and
perpendicular to both the given straight lines is the same as the straight line
passing through (3, 6,1) and parallel to 8iˆ − 6 ˆj + kˆ .
Thus, the equation of the required straight line is
is a vector perpendicular to both the given straight lines.
Therefore, the required straight line passing through (3, 6,1) and
perpendicular to both the given straight lines is the same as the straight line
passing through (3, 6,1) and parallel to 8iˆ − 6 ˆj + kˆ .
Thus, the equation of the required straight line is
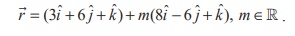
Example 6.35
Determine whether the pair of straight lines ![]() =
(2ˆi + 6ˆj + 3ˆk ) + t(2ˆi + 3ˆj + 4ˆk ) ,
=
(2ˆi + 6ˆj + 3ˆk ) + t(2ˆi + 3ˆj + 4ˆk ) , ![]() = (2ˆj − 3ˆk ) + s(ˆi + 2ˆj + 3ˆk ) are parallel. Find
the shortest distance between them.
= (2ˆj − 3ˆk ) + s(ˆi + 2ˆj + 3ˆk ) are parallel. Find
the shortest distance between them.
Solution
Comparing the given two equations with
![]() =
= ![]() + s
+ s![]() and
and ![]() =
= ![]() + t
+ t![]()
we have ![]() = 2ˆi + 6ˆj + 3ˆk,
= 2ˆi + 6ˆj + 3ˆk, ![]() = 2ˆi + 3ˆj + 4ˆk,
= 2ˆi + 3ˆj + 4ˆk, ![]() = 2ˆj − 3ˆk,
= 2ˆj − 3ˆk, ![]() = ˆi + 2ˆj + 3ˆk
= ˆi + 2ˆj + 3ˆk
Clearly, ![]() is not a scalar multiple of
is not a scalar multiple of ![]() . So, the two vectors are not parallel and hence the two lines are not
parallel.
. So, the two vectors are not parallel and hence the two lines are not
parallel.
The shortest distance between the two straight lines is given by

Therefore, the distance between the two given straight lines is
zero.Thus, the given lines intersect each other.
Example 6.36
Find the shortest distance between the two given straight lines ![]() = (2ˆi + 3ˆj + 4ˆk ) + t(−2ˆi + ˆj − 2ˆk ) and
= (2ˆi + 3ˆj + 4ˆk ) + t(−2ˆi + ˆj − 2ˆk ) and 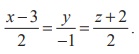
Solution
The parametric form of vector equations of the given straight
lines are
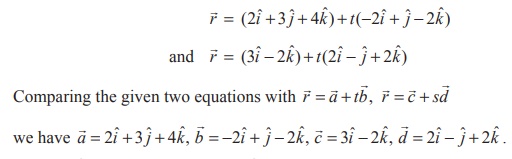
Clearly, ![]() is a scalar multiple of
is a scalar multiple of ![]() , and hence
the two straight lines are parallel. We know that the shortest distance between
two parallel straight lines is given by d
=
, and hence
the two straight lines are parallel. We know that the shortest distance between
two parallel straight lines is given by d
=
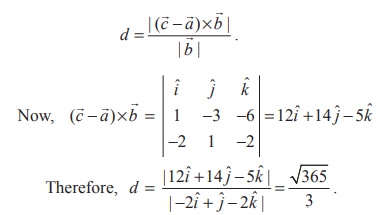
Example 6.37
Find the coordinates of the foot of the perpendicular drawn from
the point (−1, 2, 3) to the straight line ![]() = (ˆi − 4ˆj + 3ˆk ) + t(2ˆi + 3ˆj + ˆk ) . Also, find the
shortest distance from the given point to the straight line.
= (ˆi − 4ˆj + 3ˆk ) + t(2ˆi + 3ˆj + ˆk ) . Also, find the
shortest distance from the given point to the straight line.
Solution
Comparing the given equation ![]() = (ˆi - 4ˆj + 3ˆk ) + t(2ˆi + 3ˆj + ˆk ) with
= (ˆi - 4ˆj + 3ˆk ) + t(2ˆi + 3ˆj + ˆk ) with ![]() =
= ![]() + t
+ t![]() , we get
a = ˆi - 4ˆj + 3ˆk , and
, we get
a = ˆi - 4ˆj + 3ˆk , and ![]() = 2ˆi + 3ˆj + ˆk . We denote the
given point (-1, 2, 3) by D , and the point (1, -4, 3) on the straight line by
A . If F is the foot of the perpendicular from D to the straight line, then F
is of the form (2t +1, 3t - 4, t + 3) and
= 2ˆi + 3ˆj + ˆk . We denote the
given point (-1, 2, 3) by D , and the point (1, -4, 3) on the straight line by
A . If F is the foot of the perpendicular from D to the straight line, then F
is of the form (2t +1, 3t - 4, t + 3) and  = (2t + 2)iˆ + (3t - 6) ˆj + tkˆ.
= (2t + 2)iˆ + (3t - 6) ˆj + tkˆ.
Since ![]() is perpendicular to
is perpendicular to ![]() , we have
, we have
![]() .
. ![]() = 0 ⇒ 2(2t + 2) + 3(3t - 6)
+1(t) = 0
= 0 ⇒ 2(2t + 2) + 3(3t - 6)
+1(t) = 0
⇒ t = 1
Therefore, the coordinate of F
is (3,-1, 4)
Now, the perpendicular distance from the given point to the given
line is
DF = | ![]() |= √[42+(-3)2+12]
= √26 units.
|= √[42+(-3)2+12]
= √26 units.
Related Topics