Problem Questions with Answer, Solution - Exercise 6.1: Scalar Product and Vector Product | 12th Mathematics : UNIT 6 : Applications of Vector Algebra
Chapter: 12th Mathematics : UNIT 6 : Applications of Vector Algebra
Exercise 6.1: Scalar Product and Vector Product
EXERCISE 6.1
1. Prove by vector method that if a line is drawn from the centre of a circle to the midpoint of a chord, then the line is perpendicular to the chord.

2. Prove by vector method that the median to the base of an isosceles triangle is perpendicular to the base.

3. Prove by vector method that an angle in a semi-circle is a right angle.

4. Prove by vector method that the diagonals of a rhombus bisect each other at right angles.

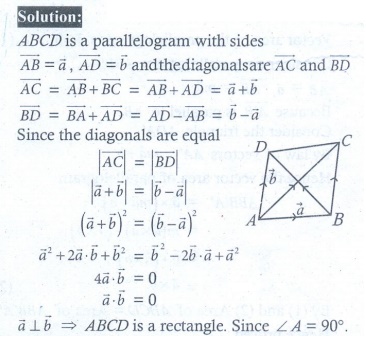
5. Using vector method, prove that if the diagonals of a parallelogram are equal, then it is a rectangle.
6. Prove by vector method that the area of the quadrilateral ABCD having diagonals AC and BD is 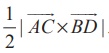 .
.

7. Prove by vector method that the parallelograms on the same base and between the same parallels are equal in area.

8. If G is the centroid of a ΔABC , prove that (area of ΔGAB) = (area of ΔGBC) = (area of ΔGCA) = 1/3 (area of ΔABC)

9. Using vector method, prove that cos(α − β ) = cosα cos β + sin α sin β .
10. Prove by vector method that sin(α + β ) = sin α cos β + cosα sin β .

11. A particle acted on by constant forces 8iˆ + 2 ˆj − 6kˆ and 6iˆ + 2 ˆj − 2kˆ is displaced from the point (1, 2, 3) to the point (5, 4,1) . Find the total work done by the forces.

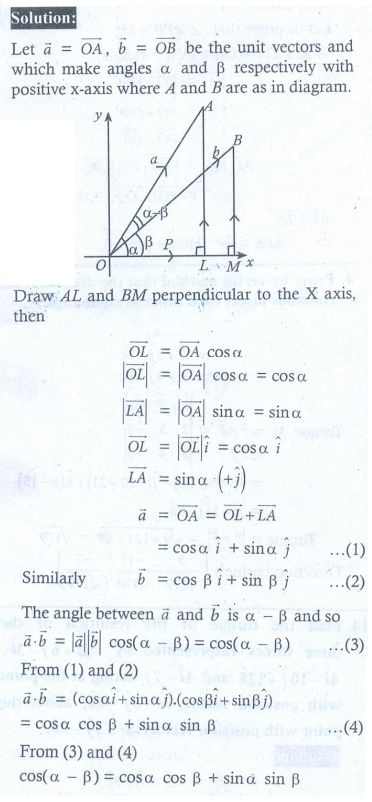
12.Forces of magnitudes 5√2 and 10√2 units acting in the directions 3iˆ + 4 ˆj + 5kˆ and 10iˆ + 6 ˆj − 8kˆ , respectively, act on a particle which is displaced from the point with position vector 4iˆ − 3 ˆj − 2kˆ to the point with position vector 6iˆ + ˆj − 3kˆ .Find the work done by the forces.
13. Find the magnitude and direction cosines of the torque of a force represented by 3iˆ + 4 ˆj − 5kˆ about the point with position vector 2iˆ − 3 ˆj +4kˆ acting through a point whose position vector is 4iˆ + 2 ˆj − 3kˆ .

14. Find the torque of the resultant of the three forces represented by −3iˆ + 6 ˆj − 3kˆ , 4iˆ −10 ˆj +12kˆ and 4iˆ + 7 ˆj acting at the point with position vector 8iˆ − 6 ˆj − 4kˆ , about the point with position vector 18iˆ + 3 ˆj − 9kˆ .
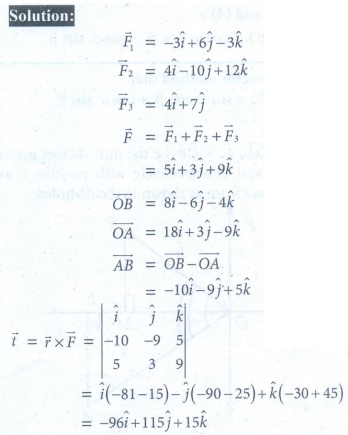
Answers:
11. 80 units
12. 69 units
13. √179 , 3/√179 , 11/√179, − , 7/√179
14. -96ˆi + 115ˆj + 15ˆk
Related Topics