Problem Questions with Answer, Solution - Exercise 6.5: Point of intersection of two straight lines | 12th Mathematics : UNIT 6 : Applications of Vector Algebra
Chapter: 12th Mathematics : UNIT 6 : Applications of Vector Algebra
Exercise 6.5: Point of intersection of two straight lines
EXERCISE 6.5
1. Find the parametric form of vector equation and Cartesian equations of a straight line passing through (5, 2, 8) and is perpendicular to the straight lines 
= (iˆ + ˆj - ˆk ) + s(2iˆ - 2 ˆj + ˆk ) and = (2iˆ - jˆ - 3kˆ ) + t(ˆi + 2 ˆj + 2ˆk ) .
2. Show that the lines = (6iˆ + ˆj + 2ˆk ) + s(iˆ + 2 ˆj - 3ˆk ) and = (3ˆi + 2 ˆj - 2ˆk ) + t(2ˆi + 4 ˆj - 5ˆk ) are skew lines and hence find the shortest distance between them.
3. If the two lines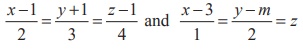 
intersect at a point, find the value of m .
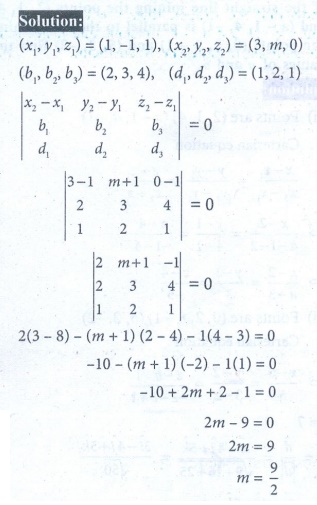
4. Show that the lines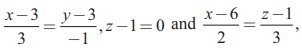 
y-2 =0 intersect. Also find the point of intersection.
5. Show that the straight lines x +1 = 2 y = -12z and x = y + 2 = 6z - 6 are skew and hence find the shortest distance between them.
6. Find the parametric form of vector equation of the straight line passing through (-1, 2,1) and parallel to the straight line = (2iˆ + 3 ˆj - kˆ) + t(iˆ - 2 ˆj + kˆ) and hence find the shortest distance between the lines.
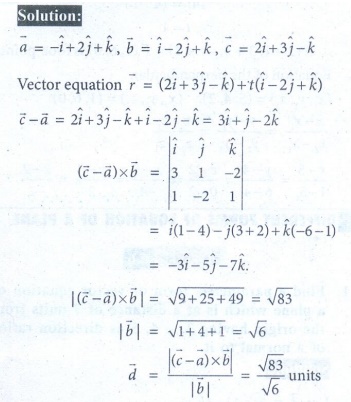
7. Find the foot of the perpendicular drawn from the point (5, 4, 2) to the line 
Also, find the equation of the perpendicular.
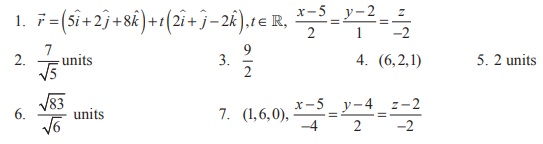
Related Topics