Definition, Theorem, Proof, Solved Example Problems, Solution - Scalar Product and Vector Product | 12th Mathematics : UNIT 6 : Applications of Vector Algebra
Chapter: 12th Mathematics : UNIT 6 : Applications of Vector Algebra
Scalar Product and Vector Product
Scalar Product and Vector Product
Next we recall the scalar product and vector product of two vectors as follows.
Definition 6.1
Given two vectors ![]() = a1iˆ + a2ˆj + a3kˆ and
= a1iˆ + a2ˆj + a3kˆ and ![]() = b1iˆ + b2ˆj + b3kˆ the scalar product (or dot product) is denoted by
= b1iˆ + b2ˆj + b3kˆ the scalar product (or dot product) is denoted by ![]() ×
× ![]() and is calculated by
and is calculated by
![]() ×
× ![]() = a1b1 + a2b2 + a3b3 ,
= a1b1 + a2b2 + a3b3 ,
and the vector product (or cross product) is denoted by ![]() ´
´ ![]() , and is calculated by
, and is calculated by

Note
![]() ×
× ![]() is a vector.
is a vector.
![]() ´
´ ![]() is a scalar, and
is a scalar, and
1. Geometrical interpretation
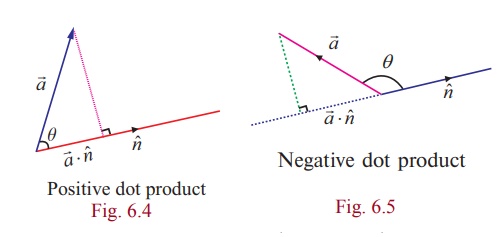
Geometrically, if ![]() is an arbitrary vector and nˆ is a unit vector, then
is an arbitrary vector and nˆ is a unit vector, then ![]() ⋅ nˆ is the projection of the vector
⋅ nˆ is the projection of the vector ![]() on the straight line on which nˆ lies. The quantity
on the straight line on which nˆ lies. The quantity ![]() ⋅ nˆ is positive if the angle between
⋅ nˆ is positive if the angle between ![]() and nˆ is acute, see Fig. 6.4 and negative if the angle between
and nˆ is acute, see Fig. 6.4 and negative if the angle between ![]() and nˆ is obtuse see Fig. 6.5.
and nˆ is obtuse see Fig. 6.5.
If ![]() and
and ![]() are arbitrary non-zero vectors, then |
are arbitrary non-zero vectors, then | ![]() ×
× ![]() | =
| = 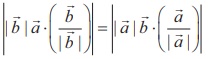 and so |
and so | ![]() ×
× ![]() | means either the length of the straight line segment obtained by projecting the vector |
| means either the length of the straight line segment obtained by projecting the vector | ![]() |
| ![]() along the direction of
along the direction of ![]() or the length of the line segment obtained by projecting the vector |
or the length of the line segment obtained by projecting the vector | ![]() |
| ![]() along the direction of
along the direction of ![]() . We recall that
. We recall that ![]() ×
× ![]() =|
=| ![]() | |
| | ![]() | cosθ , where θ is the angle between the two vectors
| cosθ , where θ is the angle between the two vectors ![]() and
and ![]() . We recall that the angle between
. We recall that the angle between ![]() and
and ![]() is defined as the measure from
is defined as the measure from ![]() to
to ![]() in the counter clockwise direction.
in the counter clockwise direction.
The vector ![]() ´
´ ![]() is either
is either ![]() or a vector perpendicular to the plane parallel to both
or a vector perpendicular to the plane parallel to both ![]() and
and ![]() having magnitude as the area of the parallelogram formed by coterminus vectors parallel to
having magnitude as the area of the parallelogram formed by coterminus vectors parallel to ![]() and
and ![]() . If
. If ![]() and
and ![]() are non-zero vectors, then the magnitude of
are non-zero vectors, then the magnitude of ![]() ´ b can be calculated by the formula
´ b can be calculated by the formula
| ![]() ´
´ ![]() | = | a | | b | | sinθ |, where θ is the angle between
| = | a | | b | | sinθ |, where θ is the angle between ![]() and
and ![]() .
.
Two vectors are said to be coterminus if they have same initial point.
Remark
(1) An angle between two non-zero vectors ![]() and
and ![]() is found by the following formula
is found by the following formula
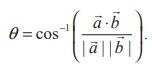
(2) ![]() and
and ![]() are said to be parallel if the angle between them is 0 or π .
are said to be parallel if the angle between them is 0 or π .
(3) ![]() and
and ![]() are said to be perpendicular if the angle between them is
are said to be perpendicular if the angle between them is 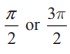
Property
(1) Let ![]() and
and ![]() be any two nonzero vectors. Then
be any two nonzero vectors. Then
![]() ⋅
⋅ ![]() = 0 if and only if
= 0 if and only if ![]() and
and ![]() are perpendicular to each other.
are perpendicular to each other.
![]() ×
× ![]() =
= ![]() if and only if
if and only if ![]() and
and ![]() are parallel to each other.
are parallel to each other.
(2) If ![]() ,
, ![]() , and c are any three vectors and α is a scalar, then
, and c are any three vectors and α is a scalar, then
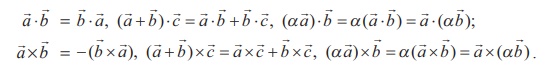
2. Application of dot and cross products in plane Trigonometry
We apply the concepts of dot and cross products of two vectors to derive a few formulae in plane trigonometry.
Example 6.1 (Cosine formulae)
With usual notations, in any triangle ABC, prove the following by vector method.
(i) a2 = b2 + c2 - 2bc cos A
(ii) b2 = c2 + a2 - 2ca cos B
(iii) c2 = a2 + b2 - 2ab cos C
Solution
With usual notations in triangle ABC, we have

a2 = b2 + c2 + 2bc cos(π - A)
a2 = b2 + c2 - 2bc cos A .
The results in (ii) and (iii) are proved in a similar way.
Example 6.2
With usual notations, in any triangle ABC, prove the following by vector method.
(i) a = b cos C + c cos B
(i) b = c cos A + a cos C
(iii) c = a cos B + b cos A
Solution
With usual notations in triangle ABC, we have ![]() = a,
= a, ![]() =
= ![]() , and
, and

⇒ a2 = ab cos C + ac cos B
Therefore a = b cos C + c cos B . The results in (ii) and (iii) are proved in a similar way.
Example 6.3
By vector method, prove that cos(α + β ) = cosα cos β − sin α sin β .
Solution
Let aˆ = ![]() and bˆ =
and bˆ = ![]() be the unit vectors and which make angles α and β , respectively, with positive x -axis, where A and B are as in the Fig. 6.8. Draw AL and BM perpendicular to the x-axis.
be the unit vectors and which make angles α and β , respectively, with positive x -axis, where A and B are as in the Fig. 6.8. Draw AL and BM perpendicular to the x-axis.

On the other hand, from (1) and (2)
aˆ ⋅ bˆ = (cosαiˆ − sin α ˆj) ⋅ (cos β iˆ + sin βˆj) = cosα cos β − sin α sin β ........(4)
From (3) and (4),
we get cos(α + β ) = cosα cos β − sin α sin β.
Example 6.4
With usual notations, in any triangle ABC, prove by vector method that 
Solution
With usual notations in triangle ABC, we have

Example 6.5
Prove by vector method that sin(α − β ) = sin α cos β − cosα sin β .
Solution
Let aˆ = ![]() and
and ![]() =
= ![]() be the unit vectors making angles α and β respectively, with positive x -axis, where A and B are as shown in the Fig. 6.10. Then, we get aˆ = cosαiˆ + sin α ˆj and bˆ = cos β iˆ + sin β ˆj ,
be the unit vectors making angles α and β respectively, with positive x -axis, where A and B are as shown in the Fig. 6.10. Then, we get aˆ = cosαiˆ + sin α ˆj and bˆ = cos β iˆ + sin β ˆj ,
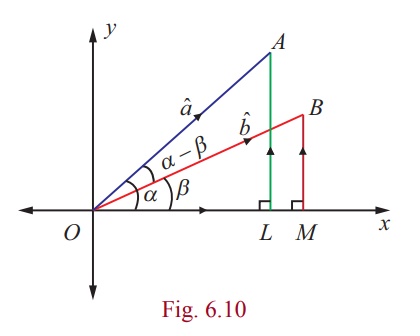
The angle between aˆ and bˆ is α − β and, the vectors bˆ, aˆ, kˆ form a right-handed system.
Hence, we get
aˆ × bˆ | bˆ | | aˆ | sin(α - β )kˆ = sin(α - β )kˆ ………………(1)
On the other hand,
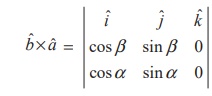 = (sin α cos β - cosα sin β )kˆ ... (2)
= (sin α cos β - cosα sin β )kˆ ... (2)
Hence, equations (1) and (2), leads to
sin(α - β ) = sin α cos β - cosα sin β .
3. Application of dot and cross products in Geometry
Example 6.6 (Apollonius's theorem)
If D is the midpoint of the side BC of a triangle ABC, show by vector method that
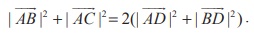
Solution
Let A be the origin, ![]() be the position vector of B and
be the position vector of B and ![]() be the position vector of C. Now D is the midpoint of BC , and so the, position vector of D is
be the position vector of C. Now D is the midpoint of BC , and so the, position vector of D is ![]()
Therefore , we have

Example 6.7
Prove by vector method that the perpendiculars (attitudes) from the vertices to the opposite sides of a triangle are concurrent.
Solution
Consider a triangle ABC in which the two altitudes AD and BE intersect at O . Let CO be produced to meet AB at F. We take O as the origin and let
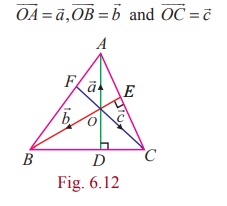
Since ![]() is perpendicular to
is perpendicular to ![]() , we have
, we have ![]() is perpendicular to
is perpendicular to ![]() , and hence we get
, and hence we get ![]() .
. ![]() = 0 . That is,
= 0 . That is, ![]() . (
. (![]() -
- ![]() ) = 0 , which means
) = 0 , which means
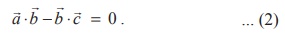
Similarly, since ![]() is perpendicular to
is perpendicular to ![]() , we have
, we have ![]() is perpendicular to
is perpendicular to ![]() , and hence we get
, and hence we get
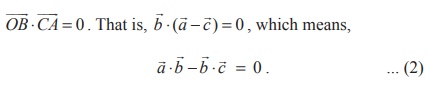
Adding equations (1) and (2), gives ![]() ⋅
⋅ ![]() −
− ![]() ⋅
⋅ ![]() = 0 . That is,
= 0 . That is, ![]() ⋅ (
⋅ (![]() −
− ![]() ) = 0 .
) = 0 .
That is, ![]() ⋅
⋅ ![]() = 0 . Therefore,
= 0 . Therefore, ![]() is perpendicular to
is perpendicular to ![]() which implies that
which implies that ![]() is perpendicular to
is perpendicular to ![]() . Hence, the perpendicular drawn from C to the side AB passes through O . Thus, the altitudes are concurrent.
. Hence, the perpendicular drawn from C to the side AB passes through O . Thus, the altitudes are concurrent.
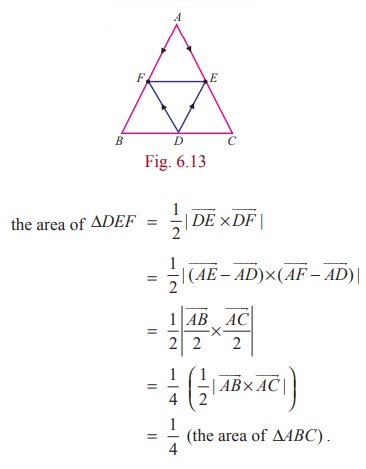
Example 6.8
In triangle ABC, the points D, E, F are the midpoints of the sides BC, CA , and AB respectively. Using vector method, show that the area of ΔDEF is equal to 1/4 (area of ΔABC).
Solution
In triangle ABC, coonsider A as the origin. Then the position vectors of D, E, F are given by
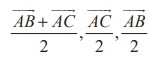
respectively. Since | ![]() × AC | is the area of the parallelogram formed by the two vectors
× AC | is the area of the parallelogram formed by the two vectors ![]() ,
, ![]() as adjacent sides, the area of ΔABC is 1/ 2 |
as adjacent sides, the area of ΔABC is 1/ 2 | ![]() |
| ![]() Similarly, considering ∆DEF , we have
Similarly, considering ∆DEF , we have
4. Application of dot and cross product in Physics
Definition 6.2
If ![]() is the displacement vector of a particle moved from a point to another point after applying a constant force
is the displacement vector of a particle moved from a point to another point after applying a constant force ![]() on the particle, then the work done by the force on the particle is w =
on the particle, then the work done by the force on the particle is w = ![]() ⋅
⋅ ![]() .
.

If the force has an acute angle, perpendicular angle, and an obtuse angle, the work done by the force is positive, zero, and negative respectively.
Example 6.9
A particle acted upon by constant forces 2iˆ + 5 ˆj + 6kˆ and −iˆ − 2 ˆj − kˆ is displaced from the point (4, −3, −2) to the point (6,1, −3) . Find the total work done by the forces.
Solution
Resultant of the given forces is ![]() = (2iˆ + 5 ˆj + 6kˆ) + (−iˆ − 2 ˆj − kˆ) = iˆ + 3 ˆj + 5kˆ.
= (2iˆ + 5 ˆj + 6kˆ) + (−iˆ − 2 ˆj − kˆ) = iˆ + 3 ˆj + 5kˆ.
Let A and B be the points (4, −3, −2) and (6,1, −3) respectively. Then the displacement vector of the particle is ![]() =
= ![]() =
= ![]() −
− ![]() = (6iˆ + ˆj − 3kˆ) − (4iˆ − 3 ˆj − 2kˆ) = 2iˆ + 4 ˆj − kˆ .
= (6iˆ + ˆj − 3kˆ) − (4iˆ − 3 ˆj − 2kˆ) = 2iˆ + 4 ˆj − kˆ .
Therefore the work done w = ![]() ⋅
⋅ ![]() = (iˆ + 3 ˆj + 5kˆ) ⋅(2iˆ + 4 ˆj − kˆ) = 9 units.
= (iˆ + 3 ˆj + 5kˆ) ⋅(2iˆ + 4 ˆj − kˆ) = 9 units.
Example 6.10
A particle is acted upon by the forces 3iˆ − 2 ˆj + 2kˆ and 2iˆ + ˆj − kˆ is displaced from the point (1, 3, −1) to the point (4, −1, λ) . If the work done by the forces is 16 units, find the value of λ .
Solution
Resultant of the given forces is ![]() = (3iˆ − 2 ˆj + 2kˆ) + (2iˆ + ˆj − kˆ) = 5iˆ − ˆj + kˆ .
= (3iˆ − 2 ˆj + 2kˆ) + (2iˆ + ˆj − kˆ) = 5iˆ − ˆj + kˆ .
The displacement of the particle is given by
![]() = (4iˆ − ˆj + λkˆ) − (iˆ + 3 ˆj − kˆ) = (3iˆ − 4 ˆj + (λ +1)kˆ) .
= (4iˆ − ˆj + λkˆ) − (iˆ + 3 ˆj − kˆ) = (3iˆ − 4 ˆj + (λ +1)kˆ) .
As the work done by the forces is 16 units, we have
![]() ⋅
⋅ ![]() = 16 .
= 16 .
That is, (5iˆ − ˆj + kˆ) ⋅ (3iˆ − 4 ˆj + (λ +1)kˆ = 16 ⇒ λ + 20 = 16 .
So, λ = −4
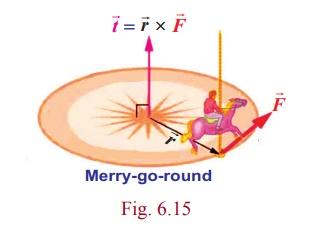
Definition 6.3
If a force ![]() is applied on a particle at a point with position vector
is applied on a particle at a point with position vector ![]() , then the torque or moment on the particle is given by
, then the torque or moment on the particle is given by ![]() =
= ![]() ×
× ![]() . The torque is also called the rotational force.
. The torque is also called the rotational force.
Example 6.11
Find the magnitude and the direction cosines of the torque about the point (2, 0, −1) of a force 2iˆ + ˆj − kˆ, whose line of action passes through the origin.
Solution
Let A be the point (2, 0, −1) . Then the position vector of A is ![]() = 2iˆ − ˆk and therefore
= 2iˆ − ˆk and therefore ![]() =
= ![]() = −2ˆi + ˆk .
= −2ˆi + ˆk .
Then the given force is ![]() = 2iˆ + ˆj − kˆ . So, the torque is
= 2iˆ + ˆj − kˆ . So, the torque is

The magnitude of the torque = | -iˆ - 2kˆ |= √5 and the direction cosines of the torque are -1/√5 , 0, -2/√5.
Related Topics