Condition for a line to lie in a plane

Condition for a line to lie in a plane

We observe that a straight line will lie in a plane if every point on the line, lie in the plane and the normal to the plane is perpendicular to the line.

i) If the line 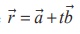 lies in the plane  â‹… = d , then  â‹…  = d and . = 0

ii) if the line 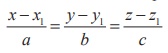 lies in the plane Ax + By + Cz + D = 0 , then

Ax₁ + By₁ + Cz₁ + D = 0 and aA + bB + cC = 0

Example 6.45

Verify whether the line 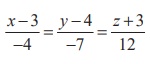 lies in the plane 5x − y + z = 8 .

Solution

Here, ( x₁, y₁, z₁ ) = (3, 4, −3) and direction ratios of the given straight line are (a,b, c) = (−4, −7,12) . Direction ratios of the normal to the given plane are ( A, B,C ) = (5, −1,1) .

We observe that, the given point ( x₁, y₁, z₁ ) = (3, 4, −3) satisfies the given plane 5x − y + z = 8

Next, aA + bB + cC = (−4)(5) + (−7)(−1) + (12)(1) = −1 ≠ 0 . So, the normal to the plane is not perpendicular to the line. Hence, the given line does not lie in the plane.