Chapter: 12th Mathematics : UNIT 6 : Applications of Vector Algebra
Intercept form of the equation of a plane
Intercept form of the equation of a plane
Let the plane ![]() ⋅
⋅ ![]() = q
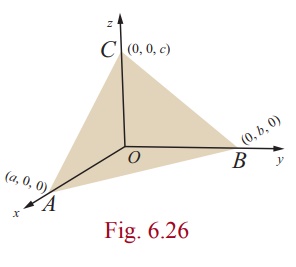
meets the coordinate axes at A,B,C respectively such that the intercepts on the axes are OA = a, OB = b, OC = c
. Now position vector of the point A is aiˆ. Since A
lies on the given plane, we have aiˆ⋅
= q
meets the coordinate axes at A,B,C respectively such that the intercepts on the axes are OA = a, OB = b, OC = c
. Now position vector of the point A is aiˆ. Since A
lies on the given plane, we have aiˆ⋅ ![]() = q which
gives
= q which
gives 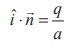 .
.
Similarly, since the vectors bˆj and cˆk lie on the given plane, we have 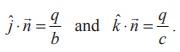 . Substituting
. Substituting
![]() = xˆi + yˆj + zˆk in
= xˆi + yˆj + zˆk in ![]() ⋅
⋅ ![]() = q
, we get
= q
, we get
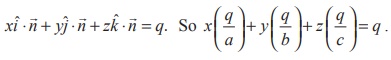
Dividing by q, we get, 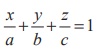 . This is called the intercept form of equation of the plane
having intercepts a, b, c on the x, y, z axes respectively.
. This is called the intercept form of equation of the plane
having intercepts a, b, c on the x, y, z axes respectively.
Theorem 6.16
The general equation ax + by + cz + d =
0 of first degree in x, y, z represents a plane.
Proof
The equation ax + by + cz + d = 0
can be written in the vector form as follows
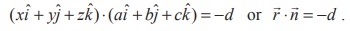
Since this is the vector form of the equation of a plane in
standard form, the given equation ax + by + cz + d = 0 represents a plane. Here
![]() = aiˆ + bˆj + ckˆ. is a vector normal to the plane.
= aiˆ + bˆj + ckˆ. is a vector normal to the plane.
Note
In the general equation ax + by + cz + d
= 0 of a plane, a, b, c are direction ratios of the normal
to the plane.
Example 6.38
Find the vector and Cartesian form of the equations of a plane
which is at a distance of 12 units from the origin and perpendicular to 6iˆ
+ 2 ˆj − 3kˆ .
Solution
Let ![]() = 6iˆ + 2 ˆj − 3kˆ
and P =12.
= 6iˆ + 2 ˆj − 3kˆ
and P =12.
If dˆ is the unit normal vector in the direction
of the vector 6iˆ + 2ˆj − 3kˆ , then
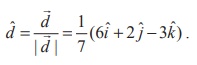
If ![]() is the position vector of an arbitrary point (x, y, z) on the plane, then using
is the position vector of an arbitrary point (x, y, z) on the plane, then using ![]() .
. ![]() = p , the vector equation of the plane in normal form is
= p , the vector equation of the plane in normal form is
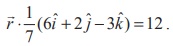
Substituting ![]() = xˆi + yˆj + zˆk in the above
equation, we get (xˆi + yˆj + zˆk ) . 1/7 (6ˆi + 2ˆ j - 3ˆk ) = 12 .
= xˆi + yˆj + zˆk in the above
equation, we get (xˆi + yˆj + zˆk ) . 1/7 (6ˆi + 2ˆ j - 3ˆk ) = 12 .
Applying dot product in the above equation and simplifying, we get
6x + 2 y − 3z = 84, which is the the standard form.
Example 6.39
If the Cartesian equation of a plane is 3x - 4 y + 3z = -8 , find the
vector equation of the plane in the standard form.
Solution
If ![]() = xi + yj + zk is the
position vector of an arbitrary point (x, y, z) on the
plane, then the given equation can be written as (xiˆ + yˆj +
zkˆ) ⋅ (3iˆ − 4 ˆj + 3kˆ) = −8 or
(xiˆ + yˆj + zkˆ) ⋅ (−3iˆ + 4 ˆj −
3kˆ) = 8 . That is,
= xi + yj + zk is the
position vector of an arbitrary point (x, y, z) on the
plane, then the given equation can be written as (xiˆ + yˆj +
zkˆ) ⋅ (3iˆ − 4 ˆj + 3kˆ) = −8 or
(xiˆ + yˆj + zkˆ) ⋅ (−3iˆ + 4 ˆj −
3kˆ) = 8 . That is, ![]() ⋅ (−3ˆi + 4ˆj −
3ˆk ) = 8 which is the vector equation of the given plane in standard
form.
⋅ (−3ˆi + 4ˆj −
3ˆk ) = 8 which is the vector equation of the given plane in standard
form.
Example 6.40
Find the direction cosines of the normal to the plane and length
of the perpendicular from the origin to the plane ![]() ⋅ (3ˆi − 4ˆ
j +12ˆk ) = 5.
⋅ (3ˆi − 4ˆ
j +12ˆk ) = 5.
Solution
Let ![]() = 3iˆ − 4 ˆj +12kˆ and
q = 5 .
= 3iˆ − 4 ˆj +12kˆ and
q = 5 .
If dˆ is the unit vector in the direction of the vector 3iˆ − 4 ˆj +12kˆ , then dˆ = 1/13 (3iˆ − 4 ˆj +12kˆ)
Now, dividing the given equation by 13 , we get
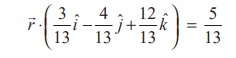
which is the equation of the plane in the normal form ![]() .ˆd = p
.ˆd = p
From this equation, we infer that 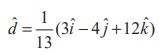 is a unit
vector normal to the plane from the origin. Therefore, the direction cosines of
dˆ are
is a unit
vector normal to the plane from the origin. Therefore, the direction cosines of
dˆ are 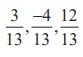 and the length of the perpendicular from the origin to the
plane is 5/13.
and the length of the perpendicular from the origin to the
plane is 5/13.
Example 6.41
Find the vector and Cartesian equations of the plane passing
through the point with position vector 4iˆ + 2 ˆj − 3kˆ
and normal to vector 2iˆ − ˆj + kˆ .
Solution
If the position vector of the given point is ![]() = 4i
+ 2 j − 3k and
= 4i
+ 2 j − 3k and ![]() = 2i − j + k ,
then the equation of the plane passing through a point and normal to a vector
is given by (
= 2i − j + k ,
then the equation of the plane passing through a point and normal to a vector
is given by (![]() −
− ![]() ) ⋅
) ⋅ ![]() = 0
or
= 0
or ![]() ⋅
⋅ ![]() =
= ![]() ⋅
⋅ ![]() .
.
Substituting ![]() = 4i + 2 j − 3k and
= 4i + 2 j − 3k and ![]() = 2i − j + k in the
above equation, we get
= 2i − j + k in the
above equation, we get
![]() = (4i + 2 j − 3k ). (2i − j + k )
= (4i + 2 j − 3k ). (2i − j + k )
Thus, the required vector equation of the plane is ![]() ⋅(2ˆi − ˆj + ˆk ) = 3 . If
⋅(2ˆi − ˆj + ˆk ) = 3 . If ![]() =
xˆi + yˆj + zˆk then we get the Cartesian
equation of the plane 2x − y + z = 3 .
=
xˆi + yˆj + zˆk then we get the Cartesian
equation of the plane 2x − y + z = 3 .
Example 6.42
A variable plane moves in such a way that the sum of the
reciprocals of its intercepts on the coordinate axes is a constant. Show that the
plane passes through a fixed point
Solution
The equation of the plane having intercepts a, b, c on
the x, y, z axes respectively is 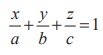 .
.
Since the sum of the reciprocals of the intercepts on the
coordinate axes is a constant, we have 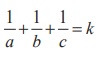 where k is a
constant, and which can be written as
where k is a
constant, and which can be written as 
This shows that the plane 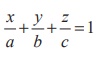 passes through the fixed point
passes through the fixed point 
Related Topics