Applications of Vector Algebra - Choose the correct answer | 12th Mathematics : UNIT 6 : Applications of Vector Algebra
Chapter: 12th Mathematics : UNIT 6 : Applications of Vector Algebra
Choose the correct answer
Choose the correct or the most suitable answer from the given four alternatives :
1. If ![]() and
and ![]() are parallel vectors, then [
are parallel vectors, then [ ![]() ,
, ![]() ,
, ![]() ] is equal to
] is equal to
(1) 2
(2) -1
(3) 1
(4) 0
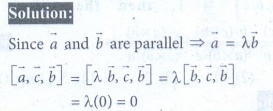
2. If a vector ![]() lies in the plane of
lies in the plane of ![]() and
and ![]() , then
, then
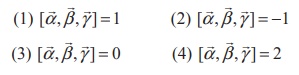
Ans: (3)

3. If 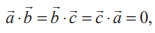 = 0, then the value of [
= 0, then the value of [![]() ,
, ![]() ,
, ![]() ] is
] is
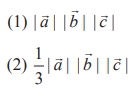
(3) 1
(4) -1
Ans: (1)

4. If ![]() ,
,![]() ,
, ![]() are three unit vectors such that
are three unit vectors such that ![]() is perpendicular to
is perpendicular to ![]() , and is parallel to
, and is parallel to ![]() then
then ![]() x (
x (![]() x
x ![]() ) is equal to
) is equal to
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
Ans: (2)
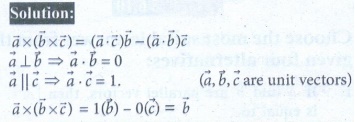
5. If [![]() ,
, ![]() ,
, ![]() ] = 1, then the value of
] = 1, then the value of 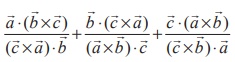 is
is
(1) 1
(2) -1
(3) 2
(4) 3
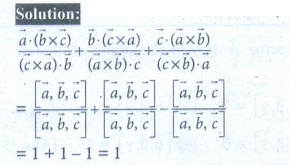
6. The volume of the parallelepiped with its edges represented by the vectors iˆ + ˆj, iˆ + 2 ˆj, iˆ + ˆj + π kˆ is
(1) π/2
(2) π/3
(3) π
(4) π/4
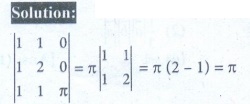
7. If ![]() and
and ![]() are unit vectors such that [
are unit vectors such that [![]() ,
, ![]() ,
, ![]() ×
× ![]() ] = π/4, then the angle between
] = π/4, then the angle between ![]() and
and ![]() is
is
(1) π/6
(2) π/4
(3) π/3
(4) π/2

8. If 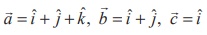 and (
and (![]() ×
× ![]() )×
)× ![]() = λ
= λ![]() + μ
+ μ![]() , then the value of λ + μ is
, then the value of λ + μ is
(1) 0
(2) 1
(3) 6
(4) 3
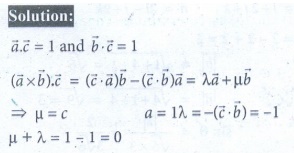
9. If ![]() ,
, ![]() ,
, ![]() are non-coplanar, non-zero vectors such that [
are non-coplanar, non-zero vectors such that [![]() ,
, ![]() ,
, ![]() ] = 3, then
] = 3, then 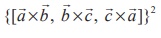 is equal to
is equal to
(1) 81
(2) 9
(3) 27
(4)18
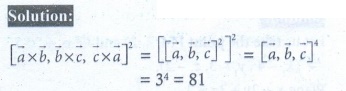
10. If ![]() ,
,![]() ,
, ![]() are three non-coplanar vectors such that
are three non-coplanar vectors such that ![]() ×(
×(![]() ×
× ![]() ) =
) = ![]() , then the angle between
, then the angle between ![]() and
and ![]() is
is
(1) π/2
(2) 3π/4
(3) π/4
(4) π

11. If the volume of the parallelepiped with ![]() ×
× ![]() ,
,![]() ×
× ![]() ,
, ![]() ×
× ![]() as coterminous edges is 8 cubic units, then the volume of the parallelepiped with (
as coterminous edges is 8 cubic units, then the volume of the parallelepiped with (![]() ×
× ![]() )×(
)×(![]() ×
× ![]() ), (
), (![]() ×
× ![]() ) ×(
) ×(![]() ×
× ![]() ) and (
) and (![]() ×
× ![]() ) ×(
) ×(![]() ×
× ![]() ) as coterminous edges is,
) as coterminous edges is,
(1) 8 cubic units
(2) 512 cubic units
(3) 64 cubic units
(4) 24 cubic units

12. Consider the vectors ![]() ,
, ![]() ,
, ![]() ,
, ![]() such that (
such that (![]() ×
× ![]() ) ×(
) ×(![]() ×
× ![]() ) = 0 . Let P1 and P2 be the planes determined by the pairs of vectors
) = 0 . Let P1 and P2 be the planes determined by the pairs of vectors ![]() ,
, ![]() and
and ![]() ,
, ![]() respectively. Then the angle between P1 and P2 is
respectively. Then the angle between P1 and P2 is
(1) 0˚
(2) 45˚
(3) 60˚
(4) 90˚

13. If ![]() ×(
×(![]() ×
×![]() ) = (
) = (![]() ×
× ![]() ) ×
) × ![]() , where
, where ![]() ,
, ![]() ,
, ![]() are any three vectors such that
are any three vectors such that ![]() .
. ![]() ≠ 0 and
≠ 0 and ![]() .
. ![]() ≠ 0 ,then
≠ 0 ,then ![]() and
and ![]() are
are
(1) perpendicular
(2) parallel
(3) inclined at an angle π/3
(4) inclined at an angle π/3

14. If ![]() = 2ˆi + 3ˆ j - ˆk,
= 2ˆi + 3ˆ j - ˆk, ![]() = iˆ + 2 ˆj - 5kˆ,
= iˆ + 2 ˆj - 5kˆ, ![]() = 3ˆi + 5 ˆj - ˆk, then a vector perpendicular to
= 3ˆi + 5 ˆj - ˆk, then a vector perpendicular to ![]() and lies in the plane containing
and lies in the plane containing ![]() and
and ![]() is
is
(1) -17iˆ + 21 ˆj - 97kˆ
(2) 17iˆ + 21 ˆj -123kˆ
(3) -17iˆ - 21 ˆj + 97kˆ
(4) -17iˆ - 21 ˆj - 97kˆ

15. The angle between the lines 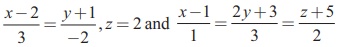 is
is
(1) π/6
(2) π/4
(3) π/3
(4) π/2
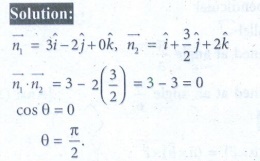
16. If the line 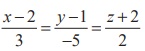 lies in the plane x + 3y - α z + β = 0, then (α , β ) is
lies in the plane x + 3y - α z + β = 0, then (α , β ) is
(1) (-5, 5)
(2) (-6, 7)
(3) (5, -5)
(4) (6, -7)

17. The angle between the line ![]() = (ˆ i + 2 ˆ j - 3 ˆ k ) + t(2 ˆ i + ˆ j - 2 ˆ k ) and the plane
= (ˆ i + 2 ˆ j - 3 ˆ k ) + t(2 ˆ i + ˆ j - 2 ˆ k ) and the plane ![]() = (ˆ i + ˆ j) + 4 = 0 is
= (ˆ i + ˆ j) + 4 = 0 is
(1) 0˚
(2) 30˚
(3) 45˚
(4) 90˚

18. The coordinates of the point where the line ![]() = (6 ˆ i - ˆ j - 3 ˆ k ) + t(-ˆ i + 4 ˆ k ) meets the plane
= (6 ˆ i - ˆ j - 3 ˆ k ) + t(-ˆ i + 4 ˆ k ) meets the plane ![]() .( ˆ i + ˆ j - ˆ k ) = 3 are
.( ˆ i + ˆ j - ˆ k ) = 3 are
(1) (2,1, 0)
(2) (7, -1, -7)
(3) (1, 2, -6)
(4) (5, -1,1)

19. Distance from the origin to the plane 3x - 6 y + 2z + 7 = 0 is
(1) 0
(2) 1
(3) 2
(4) 3
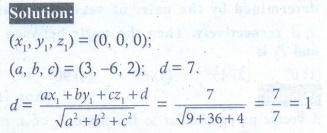
20. The distance between the planes x + 2 y + 3z + 7 = 0 and 2x + 4 y + 6z + 7 = 0 is
(1) √7 / 2√2
(2) 7/2
(3) √7 / 2
(4) 7 / 2√2

21. If the direction cosines of a line are 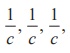 then
then
(1) c = ±3
(2) c = ±√3
(3) c > 0
(4) 0 < c < 1

22. The vector equation points ![]() = (ˆ i - 2 ˆ j - ˆ k ) + t(6 ˆ i - ˆ k ) represents a straight line passing through the
= (ˆ i - 2 ˆ j - ˆ k ) + t(6 ˆ i - ˆ k ) represents a straight line passing through the
(1) (0, 6, -1) and (1, -2, -1)
(2) (0, 6, -1) and (-1, -4, -2)
(3) (1, -2, -1) and (1, 4, -2)
(4) (1, -2, -1) and (0, -6,1)

23. If the distance of the point (1,1,1) from the origin is half of its distance from the plane x + y + z + k = 0 , then the values of k are
(1) ±3
(2) ±6
(3) -3, 9
(4) 3, -9
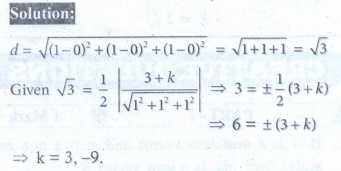
24. If the planes ![]() .(2 ˆi - λ ˆj + ˆk ) = 3 and
.(2 ˆi - λ ˆj + ˆk ) = 3 and ![]() .(4 ˆi + ˆj - μ ˆk ) = 5 are parallel, then the value of λ and μ are
.(4 ˆi + ˆj - μ ˆk ) = 5 are parallel, then the value of λ and μ are
(1) 1/2 , -2
(2) –1/2 ,2
(3) – 1/2 , -2
(4) 1/2 ,2
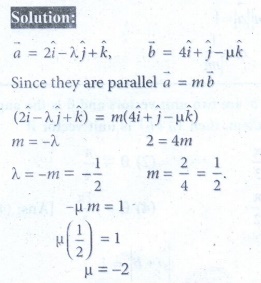
25. If the length of the perpendicular from the origin to the plane 2x + 3y + λ z = 1 , λ > 0 is 1/5 , then the value of λ is
(1) 2√3
(2) 3√2
(3) 0
(4) 1
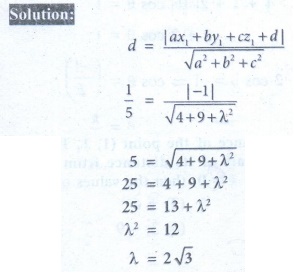
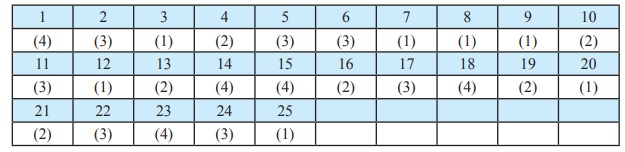
Related Topics