Definition, Solved Example Problems, Solution - Point of intersection of two straight lines | 12th Mathematics : UNIT 6 : Applications of Vector Algebra
Chapter: 12th Mathematics : UNIT 6 : Applications of Vector Algebra
Point of intersection of two straight lines
Point of intersection of two straight lines
If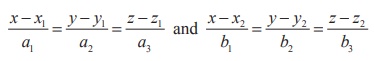 
are two lines, then every point on the
line is of the form (x1 + sa1 , y1
+ sa2 , z1 + sa3 ) and (x2
+ tb1 , y2 + tb2 , z2
+ tb3 ) respectively. If the lines are intersecting, then
there must be a common point. So, at the point of intersection, for some values
of s and t , we have
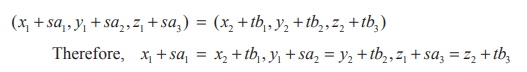
By solving any two of the above three equations, we obtain the
values of s and t . If s and t satisfy the
remaining equation, the lines are intersecting lines. Otherwise the lines are
non-intersecting . Substituting the value of s , (or by substituting the
value of t ), we get the point of intersection of two lines.
If the equations of straight lines are given in vector form, write
them in cartesian form and proceed as above to find the point of intersection.
Example 6.33
Find the point of intersection of the lines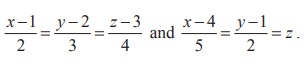 
Solution
Every point on the line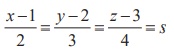 
(say) is of the form (2s +1, 3s +
2, 4s + 3) and every point on the line 
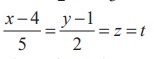(say)
is of the form (5t + 4, 2t +1, t) . So, at the point of intersection, for some values of s and t , we have
(2s +1, 3s + 2, 4s + 3) = (5t + 4, 2t +1, t)
Therefore, 2s − 5t = 3, 3s − 2t = −1
and 4s − t = −3 . Solving the first two equations we get t = −1, s = −1 .
These values of s and t satisfy the third equation. Therefore,
the given lines intersect. Substituting, these values of t or s in
the respective points, the point of intersection is (−1, −1, −1) .
Related Topics