Problem Questions with Answer, Solution - Exercise 6.6: Equation of a plane | 12th Mathematics : UNIT 6 : Applications of Vector Algebra
Chapter: 12th Mathematics : UNIT 6 : Applications of Vector Algebra
Exercise 6.6: Equation of a plane
EXERCISE 6.6
1. Find a parametric form of vector equation of a plane which is at a distance of 7 units from the origin having 3, -4, 5 as direction ratios of a normal to it.
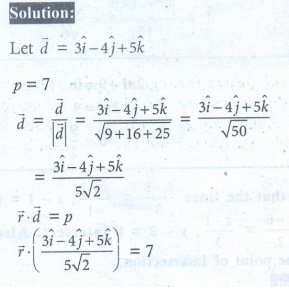
2. Find the direction cosines of the normal to the plane 12x + 3y - 4z = 65 . Also, find the non-parametric form of vector equation of a plane and the length of the perpendicular to the plane from the origin.

3. Find the vector and Cartesian equations of the plane passing through the point with position vector 2iˆ + 6 ˆj + 3kˆ and normal to the vector iˆ + 3 ˆj + 5kˆ .

4. A plane passes through the point (-1,1, 2) and the normal to the plane of magnitude 3√3 makes equal acute angles with the coordinate axes. Find the equation of the plane.

5. Find the intercepts cut off by the plane ![]() = (6ˆi + 4 ˆj - 3ˆk ) = 12 on the coordinate axes.
= (6ˆi + 4 ˆj - 3ˆk ) = 12 on the coordinate axes.

6. If a plane meets the coordinate axes at A, B, C such that the centriod of the triangle ABC is the point (u, v, w) , find the equation of the plane.

Answers:
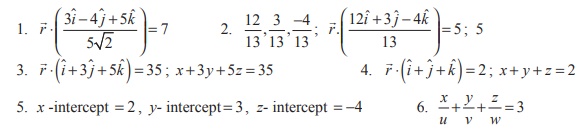
Related Topics