Terminal velocity - Viscosity

Terminal velocity

To understand terminal velocity, consider a small metallic sphere falling freely from rest through a large column of a viscous fluid.

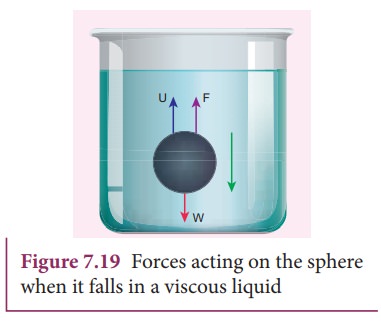
The forces acting on the sphere are (i) gravitational force of the sphere acting vertically downwards, (ii) upthrust U due to buoyancy and (iii) viscous drag acting upwards (viscous force always acts in a direction opposite to the motion of the sphere).

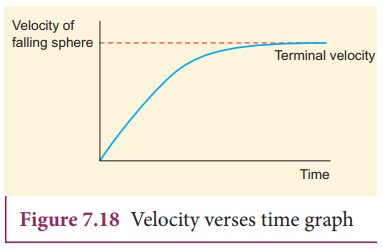
Initially, the sphere is accelerated in the downward direction so that the upward force is less than the downward force. As the velocity of the sphere increases, the velocity of the viscous force also increases. A stage is reached when the net downward force balances the upward force and hence the resultant force on the sphere becomes zero. It now moves down with a constant velocity.

The maximum constant velocity acquired by a body while falling freely through a viscous medium is called the terminal velocity VT. In the Figure 7.18, a graph is drawn with velocity along y- axis and time along x- axis. It is evident from the graph that the sphere is accelerated initially and in course of time it becomes constant, and attains terminal velocity (VT).

Expression for terminal velocity:

Consider a sphere of radius r which falls freely through a highly viscous liquid of coefficient of viscosity η. Let the density of the material of the sphere be ρ and the density of the fluid be σ.

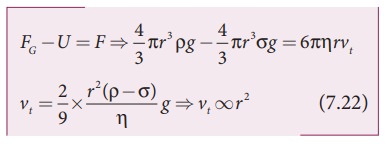
Here, it should be noted that the terminal speed of the sphere is directly proportional to the square of its radius. If σ is greater than ρ, then the term (ρ - σ) becomes negative leading to a negative terminal velocity. That is why air bubbles rise up through water or any fluid. This is also the reason for the clouds in the sky to move in the upward direction.