Properties of Matter - Elastic energy | 11th Physics : UNIT 7 : Properties of Matter
Chapter: 11th Physics : UNIT 7 : Properties of Matter
Elastic energy
Elastic
energy
When
a body is stretched, work is done against the restoring force (internal force).
This work done is stored in the body in the form of elastic energy. Consider a
wire whose un-stretch length is L and area of cross section is A. Let a force
produce an extension l and further
assume that the elastic limit of the
wire has not been exceeded and there is no loss in energy. Then, the work done
by the force F is equal to the energy gained by the wire.
The
work done in stretching the wire by dl,
dW = F dl
The
total work done in stretching the wire from 0 to l is

Substituting
equation (7.12) in equation (7.11), we get
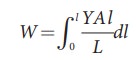
Since,
l is the dummy variable in the
integration, we can change l to lŌĆÖ (not
in limits), therefore

Energy
per unit volume is called energy density, u =

EXAMPLE 7.5
A
wire of length 2 m with the area of cross-section 10-6m2 is used to suspend a load
of 980 N. Calculate i) the stress developed in the wire ii) the strain and iii)
the energy stored.
Given:
Y = 12 ├Ś 1010NŌĆåmŌłÆ2.
Solution

Related Topics