Chapter: 11th Physics : UNIT 7 : Properties of Matter
Solved Example Problems for Surface tension
EXAMPLE 7.10
Let 2 .4├Ś10ŌłÆ4 J of work is done to increase the area of a film of soap bubble from 50 cm2 to 100 cm2. Calculate the value of surface tension of soap solution.
Solution:
A soap bubble has two free surfaces, therefore increase in surface area ŌłåA = A2ŌłÆA1 = 2(100-50) ├Ś 10-4m2 = 100 ├Ś 10-4m2.
Since, work done W = T ├Ś╬öA ŌćÆT =
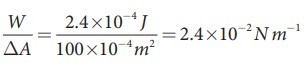
EXAMPLE 7.11
If excess pressure is balanced by a column of oil (with specific gravity 0.8) 4ŌĆåmm high, where R = 2.0ŌĆåcm, find the surface tension of the soap bubble.
Solution
The excess of pressure inside the soap

T = 15.68 ├Ś10ŌłÆ 2 N mŌłÆ1
EXAMPLE 7.12
Water rises in a capillary tube to a height of 2.0cm. How much will the water rise through another capillary tube whose radius is one-third of the first tube?
Solution
From equation (7.34), we have
h ŌłØ 1/r ŌćÆhr =constant
Consider two capillary tubes with radius r1 and r2 which on placing in a liquid, capillary rises to height h1 and h2, respectively. Then,
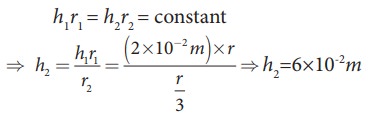
EXAMPLE 7.13
Mercury has an angle of contact equal to 140┬░ with soda lime glass. A narrow tube of radius 2ŌĆåmm, made of this glass is dipped in a trough containing mercury. By what amount does the mercury dip down in the tube relative to the liquid surface outside?. Surface tension of mercury T=0.456 NŌĆåm-1; Density of mercury Žü = 13.6 ├Ś 103 kg m-3
Solution
Capillary descent,
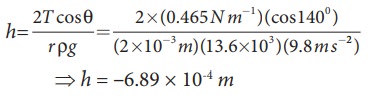
where, negative sign indicates that there is fall of mercury (mercury is depressed) in glass tube.
Related Topics