Chapter: 11th Physics : UNIT 7 : Properties of Matter
Solved Example Problems for Physics : Properties of Matter
Numerical Problems
1. A capillary of diameter dmm is dipped in water such that the water rises to a height of 30mm. If the radius of the capillary is made (2/3) of its previous value, then compute the height up to which water will rise in the new capillary?
(Answer: 45 mm)
2. A cylinder of length 1.5 m and diameter 4 cm is fixed at one end. A tangential force of 4 × 105 N is applied at the other end. If the rigidity modulus of the cylinder is 6 × 1010 N m-2 then, calculate the twist produced in the cylinder.
Solution:
Length of a cylinder =
1.5 m
Diameter = 4 cm;
Tangential force F - 4 × 105N
Rigidity modulus η = 6
× 1010 Nm-2
Twist produced θ = ?
θ = 0.053 × 10-1
= 53 × 10-4
(Answer: 45.60)
3. A spherical soap bubble A of radius 2 cm is formed inside another bubble B of radius 4 cm. Show that the radius of a single soap bubble which maintains the same pressure difference as inside the smaller and outside the larger soap bubble is lesser than radius of both soap bubbles A and B.
Solution
Excess pressure create
with S.T of spherical surface of the liquid = ΔP = 2T/R
T - surface tension
In case of soap
bubbles,
The excess pressure of
air inside them is double due to the presence of two interfaces are inside and
one outside.
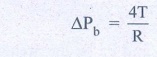
Excess pressure of air
inside the bigger bubble
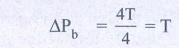
Excess pressure of air
inside the smaller bubble 4s 4T
Air pressure difference
between the smaller bubble and the atmosphere will be equal toll sum of excess
pressure inside the bigger smaller bubbles.
Pressure different ΔP =
ΔPb + ΔPs
= T + 2T = 3T
Excess pressure inside
a single soap bubble = 4T/R = 4T/4 = T
Pressure difference of
single soap bubble less than radius of both T < 3T
4. A block of Ag of mass x kg hanging from a string is immersed in a liquid of relative density 0.72. If the relative density of Ag is 10 and tension in the string is 37.12 N then compute the mass of Ag block.
Soltion
Relative density of
liquid ρliquid = 0.72
Relative density of Ag
ρAg = 10
Mass of the Ag block =
?
Tension in the string T
= 37.12 N
Apparent weight Wapp
= pAg - pliquid
= 10-0.72 = 9.28
m
=
TAg / g
m
= 37.12 / 9.28 = 4
Mass x = 4 kg
(Answer: x = 4 kg)
5. The reading of pressure meter attached with a closed pipe is 5 × 105 N m-2. On opening the valve of the pipe, the reading of the pressure meter is 4.5 × 105 Nm-2. Calculate the speed of the water flowing in the pipe.
Solution
(Answer: 10 ms-1)
Conceptual questions
1. Why coffee runs up into a sugar lump (a small cube of sugar) when one corner of the sugar lump is held in the liquid?
Answer:
(i) If sugar cube is
dropped into liquid the outermost layer has to dissolve first, then next layer,
then next until the whole sugar is dissolved.
(ii) The coffee runs up
into the pores of sugar lump due to capillary action of the liquid.
2. Why two holes are made to empty an oil tin?
Answer:
When oil comes out from
a hole of an oil tin, pressure inside it decreased than the atmosphere.
Therefore, the surrounding air rush up into the same hole prevents the oil to
come out. Hence two holes are made to empty the oil tin.
3. We can cut vegetables easily with a sharp knife as compared to a blunt knife. Why?
Answer:
Since the stress
produced on the vegetables by the sharp knife is higher than the blunt knife,
vegetables can be cut easily with the sharp knife.
4. Why the passengers are advised to remove the ink from their pens while going up in an aeroplane?
Answer:
When an aero-plane
ascends, the atmospheric pressure is decreased. Hence, the ink from the pen
will leak out. So that, the passengers are advised to remove the ink from their
pens while going up in the aero-plane.
5. We use straw to suck soft drinks, why?
Answer:
When we suck the soft
drinks through the straw, the pressure inside the straw becomes less than the
atmospheric pressure. Due to the difference in pressure, the soft drink rises
in the straw and we are able to enjoy it conveniently.
EXAMPLE 7.1
Within the elastic limit, the stretching strain produced in wires A, B, and C due to stress is shown in the figure. Assume the load applied are the same and discuss the elastic property of the material.
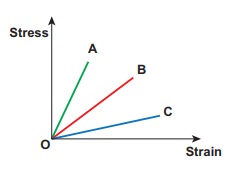
Write down the elastic modulus in ascending order.
Solution
Here, the elastic modulus is Young modulus and due to stretching, stress is tensile stress and strain is tensile strain.
Within the elastic limit, stress is proportional to strain (obey Hooke’s law). Therefore, it shows a straight line behavior. So, the modulus of elasticity (here, Young modulus) can be computed by taking slope from this straight line. Hence, calculating the slope for the straight line, we get
Slope of A > Slope of B > Slope of C
Which implies,
Young modulus of C < Young modulus of B < Young modulus of A
Notice that larger the slope, lesser the strain (fractional change in length). So, the material is much stiffer. Hence, the elasticity of wire A is greater than wire B which is greater than C. From this example, we have understood that Young’s modulus measures the resistance of solid to a change in its length.
EXAMPLE 7.2
A wire 10 m long has a cross-sectional area 1.25 x 10-4 m2. It is subjected to a load of 5 kg. If Young’s modulus of the material is 4 x 1010 N m-2, calculate the elongation produced in the wire.
Take g = 10 ms-2.
Solution
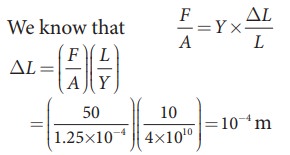
EXAMPLE 7.3
A metallic cube of side 100 cm is subjected to a uniform force acting normal to the whole surface of the cube. The pressure is 106 pascal. If the volume changes by 1.5 x 10-5 m3, calculate the bulk modulus of the material.
Solution
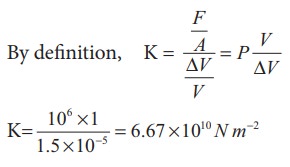
EXAMPLE 7.4
A metal cube of side 0.20 m is subjected to a shearing force of 4000 N. The top surface is displaced through 0.50 cm with respect to the bottom. Calculate the shear modulus of elasticity of the metal.
Solution
Here, L = 0.20 m, F = 4000 N, x = 0.50 cm
= 0.005 m and Area A = L2 = 0.04 m2
Therefore, Shear modulus
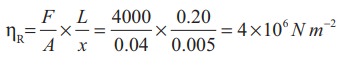
EXAMPLE 7.5
A wire of length 2 m with the area of cross-section 10-6m2 is used to suspend a load of 980 N. Calculate i) the stress developed in the wire ii) the strain and iii) the energy stored.
Given: Y = 12 × 1010N m−2.
Solution
EXAMPLE 7.6
A solid sphere has a radius of 1.5 cm and a mass of 0.038 kg. Calculate the specific gravity or relative density of the sphere.
Solution
Radius of the sphere R = 1.5 cm
mass m = 0.038 kg
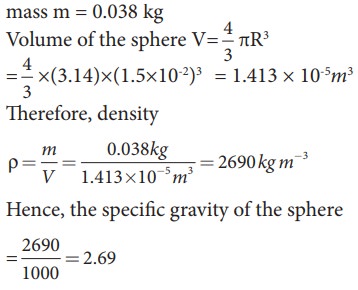
Solved Example Problems for Pascal’s law
EXAMPLE 7.7
Two pistons of a hydraulic lift have diameters of 60 cm and 5 cm. What is the force exerted by the larger piston when 50 N is placed on the smaller piston?
Solution
Since, the diameter of the pistons are given, we can calculate the radius of the piston
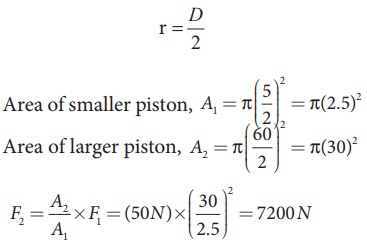
This means, with the force of 50 N, the force of 7200 N can be lifted.
EXAMPLE 7.8
A cube of wood floating in water supports a 300 g mass at the centre of its top face. When the mass is removed, the cube rises by 3 cm. Determine the volume of the cube.
Solution
Let each side of the cube be l. The volume occupied by 3 cm depth of cube,
V=(3cm) × l2 = 3l2cm
According to the principle of floatation, we have
Vρg = mg ⇒ Vρ = m
ρ is density of water = 1000 kg m-3
(3l2 × 10-2m) × (1000 kgm-3)=300 × 10-3 kg
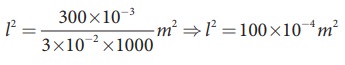
l = 10 × 10-2m = 10 cm
Therefore, volume of cube V = l3 = 1000 cm3
EXAMPLE 7.9
A metal plate of area 2.5×10-4m2 is placed on a 0.25×10-3m thick layer of castor oil. If a force of 2.5 N is needed to move the plate with a velocity 3×10-2m s-1, calculate the coefficient of viscosity of castor oil.
Given: A=2.5×10-4 m2, dx = 0.25×10-3m, F=2.5N and dv = 3×10-2 m s-1
Solution
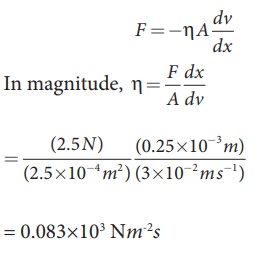
EXAMPLE 7.10
Let 2 .4×10−4 J of work is done to increase the area of a film of soap bubble from 50 cm2 to 100 cm2. Calculate the value of surface tension of soap solution.
Solution:
A soap bubble has two free surfaces, therefore increase in surface area ∆A = A2−A1 = 2(100-50) × 10-4m2 = 100 × 10-4m2.
Since, work done W = T ×ΔA ⇒T =
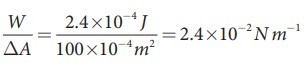
EXAMPLE 7.11
If excess pressure is balanced by a column of oil (with specific gravity 0.8) 4 mm high, where R = 2.0 cm, find the surface tension of the soap bubble.
Solution
The excess of pressure inside the soap
T = 15.68 ×10− 2 N m−1
EXAMPLE 7.12
Water rises in a capillary tube to a height of 2.0cm. How much will the water rise through another capillary tube whose radius is one-third of the first tube?
Solution
From equation (7.34), we have
h ∝ 1/r ⇒hr =constant
Consider two capillary tubes with radius r1 and r2 which on placing in a liquid, capillary rises to height h1 and h2, respectively. Then,
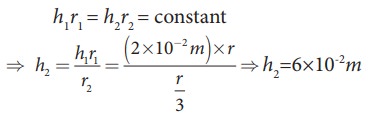
EXAMPLE 7.13
Mercury has an angle of contact equal to 140° with soda lime glass. A narrow tube of radius 2 mm, made of this glass is dipped in a trough containing mercury. By what amount does the mercury dip down in the tube relative to the liquid surface outside?. Surface tension of mercury T=0.456 N m-1; Density of mercury ρ = 13.6 × 103 kg m-3
Solution
Capillary descent,
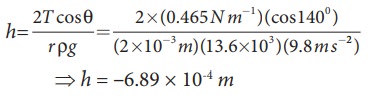
where, negative sign indicates that there is fall of mercury (mercury is depressed) in glass tube.
EXAMPLE 7.14
In a normal adult, the average speed of the blood through the aorta (radius r = 0.8 cm) is 0.33 ms-1. From the aorta, the blood goes into major arteries, which are 30 in number, each of radius 0.4 cm. Calculate the speed of the blood through the arteries.
Solution:
a1v1 = 30 a2 v2 ⇒ π r12v1 = 30 π r22v2
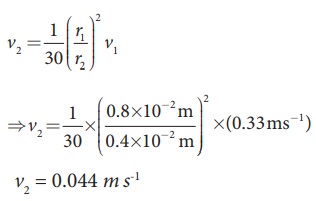
Related Topics