Chapter: 11th Physics : UNIT 7 : Properties of Matter
HookeŌĆÖs law and its experimental verification
HookeŌĆÖs
law and its experimental verification
HookeŌĆÖs
law is for a small deformation, when the stress and strain are proportional to
each other. It can be verified in a simple way by stretching a thin straight
wire (stretches like spring) of length L and uniform cross-sectional area A
suspended from a fixed point O. A pan and a pointer are attached at the free
end of the wire as shown in Figure 7.7 (a). The extension produced on the wire
is measured using a vernier scale arrangement. The experiment shows that for a
given load, the corresponding stretching force is F and the elongation produced
on the wire is ΔL. It is directly proportional to the original length L and
inversely proportional to the area of cross section A. A graph is plotted using
F on the X- axis and ΔL on the Y- axis. This graph is a straight line passing
through the origin as shown in Figure 7.7 (b).


Therefore,
ŌłåL = (slope)F
Multiplying
and dividing by volume,
V
= A L,

Comparing
with equation (7.1) and equation (7.2), we get equation (7.5) as
Žā ŌłØ ╬Ą
i.e.,
the stress is proportional to the strain in the elastic limit.
Stress ŌĆō Strain profile curve:
The
stress versus strain profile is a plot in which stress and strain are noted for
each load and a graph is drawn taking strain along the X-axis and stress along
the Y-axis. The elastic characteristics of the materials can be analyzed from
the stress-strain profile.
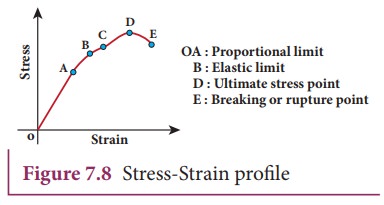
(a) Portion OA:
In
this region, stress is very small such that stress is proportional to strain,
which means HookeŌĆÖs law is valid. The point A is called limit of proportionality because
above this point HookeŌĆÖs law is not
valid. The slope of the line OA gives the YoungŌĆÖs modulus of the wire.
(b) Portion AB:
This
region is reached if the stress is increased by a very small amount. In this
region, stress is not proportional to the strain. But once the stretching force
is removed, the wire will regain its original length. This behaviour ends at
point B and hence, the point B is known as yield
point (elastic limit). The elastic behaviour of the material (here wire) in
stress-strain curve is OAB.
(c) Portion BC:
If
the wire is stretched beyond the point B (elastic limit), stress increases and
the wire will not regain its original length after the removal of stretching
force.
(d) Portion CD:
With
further increase in stress (beyond the point C), the strain increases rapidly
and reaches the point D. Beyond D, the strain increases even when the load is
removed and breaks (ruptures) at the point E. Therefore, the maximum stress
(here D) beyond which the wire breaks is called breaking stress or tensile
strength. The corresponding point D
is known as fracture point. The
region BCDE represents the plastic behaviour of the material of the wire.
Related Topics