Properties of Matter - Moduli of elasticity | 11th Physics : UNIT 7 : Properties of Matter
Chapter: 11th Physics : UNIT 7 : Properties of Matter
Moduli of elasticity
Moduli of elasticity
From HookeŌĆÖs law, the stress in a body is proportional to the corresponding strain, provided the deformation is very small. In this section, we shall define the elastic modulus of a given material. There are three types of elastic modulus.
![]()
![]() (a) YoungŌĆÖs modulus
(a) YoungŌĆÖs modulus
(b) Rigidity modulus (or Shear modulus)
(c) Bulk modulus
1. YoungŌĆÖs modulus:
When a wire is stretched or compressed, then the ratio between tensile stress (or compressive stress) and tensile strain (or compressive strain) is defined as YoungŌĆÖs modulus.

The unit for Young modulus has the same unit of stress because, strain has no unit. So, S.I. unit of Young modulus is N m-2 or pascal.
EXAMPLE 7.1
Within the elastic limit, the stretching strain produced in wires A, B, and C due to stress is shown in the figure. Assume the load applied are the same and discuss the elastic property of the material.
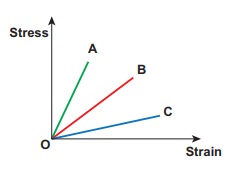
Write down the elastic modulus in ascending order.
Solution
Here, the elastic modulus is Young modulus and due to stretching, stress is tensile stress and strain is tensile strain.
Within the elastic limit, stress is proportional to strain (obey HookeŌĆÖs law). Therefore, it shows a straight line behavior. So, the modulus of elasticity (here, Young modulus) can be computed by taking slope from this straight line. Hence, calculating the slope for the straight line, we get
Slope of A > Slope of B > Slope of C
Which implies,
Young modulus of C < Young modulus of B < Young modulus of A
Notice that larger the slope, lesser the strain (fractional change in length). So, the material is much stiffer. Hence, the elasticity of wire A is greater than wire B which is greater than C. From this example, we have understood that YoungŌĆÖs modulus measures the resistance of solid to a change in its length.
EXAMPLE 7.2
A wire 10 m long has a cross-sectional area 1.25 x 10-4 m2. It is subjected to a load of 5 kg. If YoungŌĆÖs modulus of the material is 4 x 1010 NŌĆåm-2, calculate the elongation produced in the wire.
Take g = 10 ms-2.
Solution
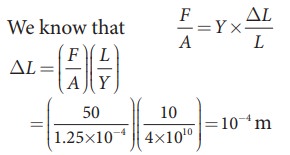
2. Bulk modulus:
Bulk modulus is defined as the ratio of volume stress to the volume strain.
Bulk modulus, K =
Normal ( Perpendicular )stress or Pressure / Volume strain
The normal stress or pressure is
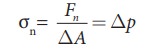
The volume strain is
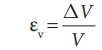
Therefore, Bulk modulus is
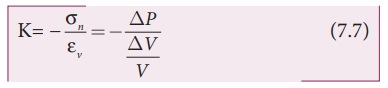
The negative sign in the equation (7.7) means that when pressure is applied on the body, its volume decreases. Further, the equation (7.7) implies that a material can be easily compressed if it has a small value of bulk modulus. In other words, bulk modulus measures the resistance of solids to change in their volume. For an example, we know that gases can be easily compressed than solids, which means, gas has a small value of bulk modulus compared to solids. The S.I. unit of K is the same as that of pressure i.e., NŌĆåm-2 or Pa (pascal).
Compressibility
The reciprocal of the bulk modulus is called compressibility. It is defined as the fractional change in volume per unit increase in pressure.
From the equation (7.7) we can say that the compressibility
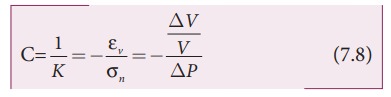
Since, gases have small value of bulk modulus than solids, their, values of compressibility is very high.
After pumping the air in the cycle tyre, usually we press the cycle tyre to check whether it has enough air. What is checked here is essentially the compressibility of air. The tyre should be less compressible for its easy rolling

In fact the rear tyre is less compressible than front tyre for a smooth ride
EXAMPLE 7.3
A metallic cube of side 100 cm is subjected to a uniform force acting normal to the whole surface of the cube. The pressure is 106pascal. If the volume changes by 1.5 x 10-5 m3, calculate the bulk modulus of the material.
Solution
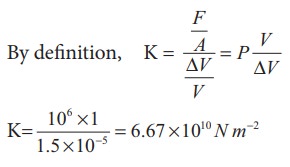
3. The rigidity modulus or shear modulus:
The rigidity modulus is defined as Rigidity modulus or Shear modulus,

Therefore, Rigidity modulus is
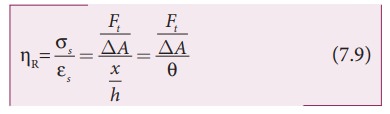
Further, the equation (7.9) implies, that a material can be easily twisted if it has small value of rigidity modulus. For example, consider a wire, when it is twisted through an angle ╬Ė, a restoring torque is developed, that is
Žä ŌłØ ╬Ė
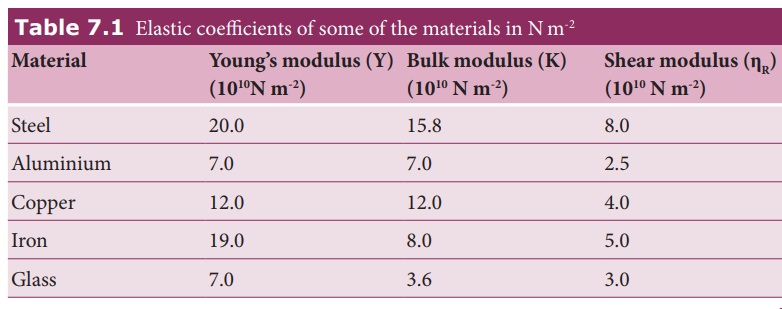
This means that for a larger torque, wire will twist by a larger amount (angle of shear ╬Ė is large). Since, rigidity modulus is inversely proportional to angle of shear, the modulus of rigidity is small. The S.I. unit of ╬ĘR is the same as that of pressure i.e., NŌĆåm-2 or pascal. For the best understanding, the elastic coefficients of some of the important materials are listed in Table 7.1.
EXAMPLE 7.4
A metal cube of side 0.20 m is subjected to a shearing force of 4000 N. The top surface is displaced through 0.50 cm with respect to the bottom. Calculate the shear modulus of elasticity of the metal.
Solution
Here, L = 0.20 m, F = 4000 N, x = 0.50 cm
= 0.005 m and Area A = L2 = 0.04 m2
Therefore, Shear modulus
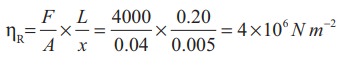
Related Topics