Properties of Matter | Physics - Long Questions and Answer | 11th Physics : UNIT 7 : Properties of Matter
Chapter: 11th Physics : UNIT 7 : Properties of Matter
Long Questions and Answer
Properties of Matter (Physics)
Long Answer Questions
1. State HookeŌĆÖs law and verify it with the help of an experiment.
1)
For a small deformation, within the elastic limit the stress and strain are
proportional to each other.
2)
It can be verified by stretching a thin straight wire (stretches like spring)
of length L and uniform cross-sectional area A suspended from a fixed point O.
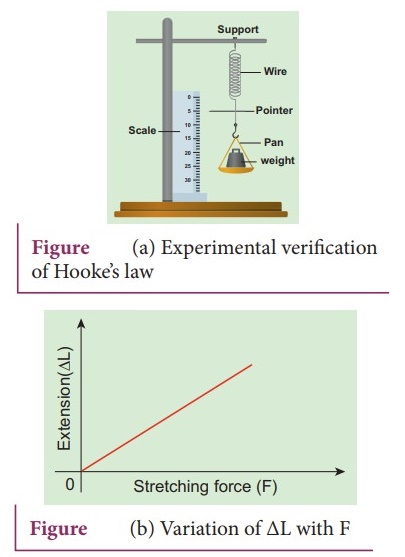
3)
A pan and a pointer are attached at the free end of the wire as shown in Figure
(a).
4)
The extension produced on the wire is measured using a vernier scale
arrangement. The experiment shows that for a given load, the corresponding
stretching force is F and the elongation produced on the wire is ŌłåL.ŌĆā
5)
It is directly proportional to the original length L and inversely proportional
to the area of cross section A. A graph is plotted using F on the X-axis and ŌłåL
on the Y-axis.
6)
This graph is a straight line passing through the origin as shown in Figure
(b). Therefore.
ŌłåL
= (slope) F Multiplying and dividing by volume.
V
= A L
F
(slope) = [AL / AL] ŌłåL
Rearranging,
we get, F / A = (L / A(slope) ) ŌłåL/ L
Therefore,
F/A ŌłØ ( ŌłåL/L)
Comparing
with stress equation, the stress is proportional to the strain in the elastic
limit.
2. Explain the different types of modulus of elasticity.
There
are three types of elastic modulus.
(a)
Young's modulus, (b) Rigidity modulus (or shear modulus) (c) Bulk modulus.
Young's
modulus:
ŌŚÅ
When a wire is stretched or compressed, then the ratio between tensile stress
(or compressive stress) and tensile strain (or compressive strain) is defined
as Young's modulus.
Y = Tensile stress or compressive stress / Tensile stress or compressive strain
ŌŚÅ
The unit for young modulus has the same unit of stress because, strain has no
unit. So S.I. unit of Young modulus is N m-2 or pascal.
Bulk
modulus:
ŌŚÅ
Bulk modulus is defined as the ratio of volume stress to the volume strain:
ŌŚÅ
Bulk modulus, K = Normal (Perpendicular) stress or pressure / Volume strain
ŌŚÅ
The normal stress or pressure is on Žān = Fn
/ ΔA = Δp
ŌŚÅ
The volume strain is ╬Ąv = ╬öV / V
ŌŚÅ
Therefore, Bulk modulus is K = ŌłÆ Žān / ╬Ąv = ŌłÆ (╬öp) / (╬öV/V)
ŌŚÅ
The negative sign in the equation means that when pressure is applied on the
body, its volume decreases. A material can be easily compressed if it has a
small value of bulk modulus.
The
rigidity modulus or shear modulus:
ŌŚÅ
The rigidity modulus is defined as Rigidity modulus or shear modulus.
╬ĘR
= Shearing stress / Angle of shear or shearing strain
ŌŚÅ
The shearing stress is Žās = tangential force / area over which it is
applied = Ft / ΔA
ŌŚÅ The angle of shear or shearing strain ╬Ąs = x / h = ╬Ė
ŌŚÅ Therefore, Rigidity modulus is ╬ĘR= Žā / ╬Ąs

ŌŚÅ A material can be easily twisted if it has small value of rigidity modulus.
ŌŚÅ Consider a wire, when it is twisted through an angle , a restoring torque is developed ŌĆ”ŌĆ”..Žä ╬▒ ╬Ė
ŌŚÅ For a larger torque, wire will twist by a larger amount (angle of shear ╬Ė is large). Since, rigidity modulus is inversely proportional to angle of shear, the modulus of rigidity is small.
3. Derive an expression for the elastic energy stored per unit volume of a wire.
ŌŚÅ
When a body is stretched, work is done against the restoring force (internal
force).
ŌŚÅ
This work done is stored in the body in the form of elastic energy.
ŌŚÅ
Consider a wire whose un-stretch length is L and area of cross section is A.
ŌŚÅ
Let a force produce an extension ØæÖ and
further assume that the elastic limit of the wire has not been exceeded and
there is no loss in energy.
ŌŚÅ
Then the work done by the force F is equal to the energy gained by the wire.
ŌŚÅ
The work done in stretching the wire by dØæÖ, dW = F
dØæÖ
ŌŚÅ
The total work done in stretching the wire from 0 to 1 is
W
= ╩ā10 FdØæÖ ŌĆ”ŌĆ”ŌĆ”.. (1)
ŌŚÅ
From Young's modulus of elasticity.
Y
= F/A ├Ś L/ØæÖ
ŌćÆ F = YAØæÖ / L ŌĆ”ŌĆ”ŌĆ”ŌĆ”.(2)
ŌŚÅ
Substituting equation (2) in equation (1). We get W = ╩ā10 YAØæÖ / L dØæÖ = YAØæÖ2/ L.2
= 1/2 FØæÖ

W
= 1/2 FØæÖ =
Elastic potential energy.
Energy
per unit volume is called energy density.
u =
Elastic potential energy / Volume

=
1/ 2 (Stress ├Ś Srain)
4. Derive an equation for the total pressure at a depth ŌĆśhŌĆÖ below the liquid surface.
ŌŚÅ
Consider a water sample of cross sectional area in the form of a cylinder. Let h1
and h2 be the depths from the air-water interface to level 1
and level 2 of the cylinder, respectively as shown in Figure (a).
ŌŚÅ
Let F1 be the force acting downwards on level 1 and F2 be
the force acting upwards on level 2.
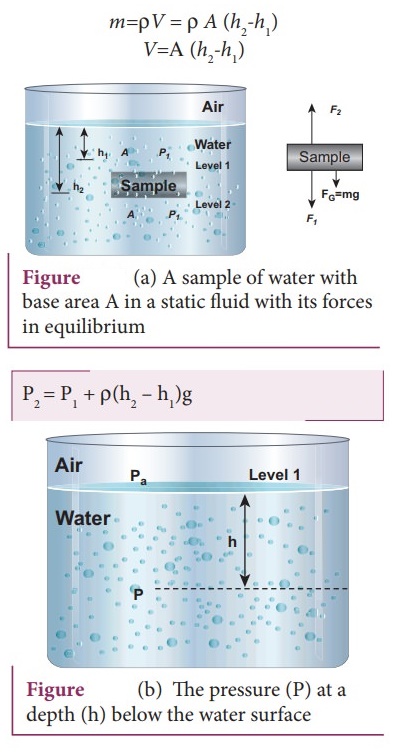
ŌŚÅ
Such that, F1 = P1A and F2 = P2A . Let
us assume the mass of the sample to be m.
ŌŚÅ
Under equilibrium condition the total upward force (F2) is balanced
by the total downward force (F1 + mg). The gravitational force will
act downward which is being exactly balanced by the difference between the
force. F2 ŌĆō F1.
F2
ŌĆō F1. = mg = FG
ŌŚÅ
Where m is the mass of the water available in the sample element. Let Žü be the
density of the water then, the mass of water available in the sample element is
m = ŽüV = ŽüA(h2 ŌĆō h1) Hence, gravitational force.
FG
= ŽüA(h2 ŌĆō h1) g
ŌŚÅ
On substituting the value of FG in equation
F2
= F1 + mg
=> P2A = P1A + ŽüA (h2
ŌĆō h1) g
Cancelling
out A on both sides, P2 = P1 + Žü (h2 ŌĆō h1)
g
ŌŚÅ
If we choose the level 1 at the surface of the liquid (i.e., air-water
interface) and the level 2 at a depth 'h' below the surface (as shown in Figure
(b), then the value of h1 becomes zero (h1=0) and in turn
P1 assumes the value of atmospheric pressure (Pa).
ŌŚÅ
The pressure (P2) at a depth becomes P. Substituting these values in
equation, we get P = Pa + Žügh
ŌŚÅ
The pressure at a depth h is greater than the pressure on the surface on the
liquid, where Pa is the atmospheric pressure which is equal to 1.013
├Ś 105 Pa.
ŌŚÅ If the atmospheric pressure is neglected or ignored then P = Žügh
5. State and prove PascalŌĆÖs law in fluids.

ŌŚÅ
Hydraulic lift which is used to lift a heavy load with a small force.
It
is a force multiplier.
ŌŚÅ
It consists of two cylinders A and B connected to each other by a horizontal
pipe, filled with a liquid.
ŌŚÅ
They are fitted with frictionless pistons of cross sectional areas A1
and A2 (A2 > A1).
ŌŚÅ
A downward force F is applied on the smaller piston.
ŌŚÅ
The pressure of the liquid under this piston increases to P, where
P = F1 / A1
ŌŚÅ
But according to Pascal's law, this increased pressure P is transmitted
undiminished in all directions.
ŌŚÅ
So a pressure is exerted on piston B.
ŌŚÅ
Upward force on piston B is F2 = P ├Ś A2
= [ F1/A1 ] ├Ś A2 ŌćÆ F2 = [ A2/A1
] ├Ś F1
ŌŚÅ Therefore by changing the force on the smaller piston A, the force on the piston B has been increased by the factor A2/A1 and this factor is called the mechanical advantage of the lift.
6. State and prove Archimedes principle.
It
states that when a body is partially or wholly immersed in a fluid, it
experiences an upward thrust equal to the weight of the fluid displaced by it
and its up-thrust acts through the centre of gravity of the liquid displaced.
Up-thrust
or buoyant force = weight of liquid displaced.

7. Derive the expression for the terminal velocity of a sphere moving in a high viscous fluid using stokes force.
ŌŚÅ
Expression for terminal velocity.
ŌŚÅ
Consider a sphere of radius r which falls freely through a highly viscous
liquid of coefficient of viscosity ╬Ę. Let the density of the material of the
sphere be Žü and the density of the fluid be Žā.
ŌŚÅ
Gravitational force acting on the sphere.
ŌŚÅ
FG = mg = 4/3 ŽĆr3 Žüg
(downward force) Up thrust, U = 4/3 ŽĆr3 Žāg (upward
force) viscous force
ŌŚÅ
At terminal velocity u,
ŌŚÅ
downward force = upward force
FG ŌĆō U = F
ŌćÆ 4/3 ŽĆr3 Žüg
ŌĆō 4/3 ŽĆr3 Žāg = 6ŽĆ╬Ęrvt
vt
= [2/9] ├Ś [r2 (Žü ŌĆō Žā) / ╬Ę]g ŌćÆ vt Ōł× r2
ŌŚÅ The terminal speed of the sphere is directly proportional to the square of its radius. If Žā is greater than Žü. then the term (Žü - Žā) becomes negative leading to a negative terminal velocity.
8. Derive PoiseuilleŌĆÖs formula for the volume of a liquid flowing per second through a pipe under streamlined flow.
ŌŚÅ
Consider a liquid flowing steadily through a horizontal capillary tube.
ŌŚÅ
Let v = ( V / t ) be the volume of the liquid flowing out per
second through a capillary tube.
ŌŚÅ
It depends on (1) coefficient of viscosity (╬Ę) of the liquid. (2) radius of the
tube (r), and (3) the pressure gradient (P / l).
ŌŚÅ
Then, vŌł×╬Ęarb(P / l)c
; v = k╬Ęarb(P/l)c
ŌĆ”ŌĆ”ŌĆ”..(1)
Where
k is a dimensionless constant.
Therefore,
[v] = volume / time = [ L3TŌĆō1],
[
dP / dx ] = Presence / distance = [MLŌĆō2TŌĆō2],
[╬Ę]=[
MLŌĆō1TŌĆō1] and [r] = [L]
Substituting
in equation (1) we get,
[L3TŌłÆ1]
= [MLŌłÆ1TŌłÆ1]a [L]b [MLŌłÆ2T2]c
[M0L3TŌłÆ1]
= Ma+c LŌłÆa+bŌłÆ2c TŌłÆaŌłÆ2c
So,
equating the powers of M,L, and T on both sides, we get a+c=0, ŌłÆa+bŌłÆ2c = 3, and
ŌłÆaŌłÆ2c = ŌłÆ1.
ŌŚÅ
Solving these equations, we get a = ŌłÆ1, b = 4 and c = 1.
ŌŚÅ
Therefore, equation becomes, v = k╬ĘŌłÆ1r4 (P/l)1
The
value of k = ŽĆ / 8
Ōł┤ v = ŽĆr4P
/ 8╬Ęl ŌĆ”ŌĆ”ŌĆ”ŌĆ”(2)
9. Obtain an expression for the excess of pressure inside a i) liquid drop ii) liquid bubble iii) air bubble.
i)
Excess pressure inside the liquid drop
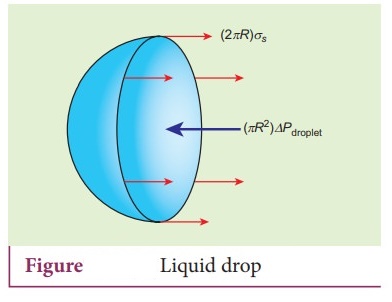
Consider
a liquid drop of radius R and the surface tension of the liquid is T as shown
in Figure.
The
various forces acting on the liquid drop are,
i)
Force due to surface tension FT = 2ŽĆRT towards right
ii)
Force due to outside pressure FP1 = P1ŽĆR2
towards right
iii)
Force due to inside pressure FP2 = P2ŽĆR2
towards left
As the drop is in equilibrium, FP2 = FT + Fp1
P2ŽĆR2
= 2ŽĆRT + P1ŽĆR2
=> (P2 ŌĆō P1 )ŽĆR2 = 2ŽĆRT
Excess pressure is ŌłåP = P2 ŌĆō P1 = 2T / R
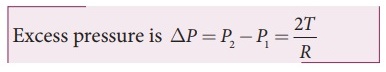
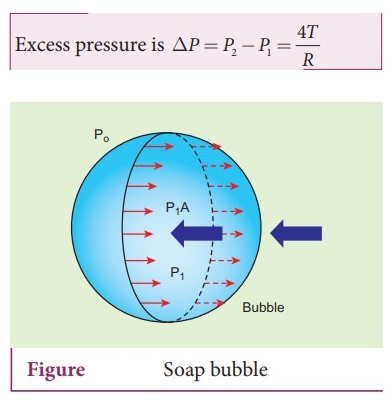
ii)
Excess pressure inside a soap bubble.
Consider
a soap bubble of radius R and the surface tension of the soap bubble be T. A
soap bubble has two liquid surfaces in contact with air, one inside the bubble
and other outside the bubble.
Therefore
the force on the soap bubble due to surface tension is 2 ├Ś 2ŽĆRT. The various
forces acting on the soap bubble are,
i)
Force due to surface tension FT = 4ŽĆRT towards right
ii)
Force due to outside pressure Fp1 = P1ŽĆR2
towards right
iii)
Force due to inside pressure Fp2 = P2ŽĆR2
towards left
As
the bubble is in equilibrium, Fp2 = FT + Fp1
P2ŽĆR2
= 4ŽĆRT + P1ŽĆR2
=>
(P2 ŌĆō P1 ) ŽĆR2 = 4ŽĆRT
Excess
pressure is ŌłåP = P2 ŌłÆ P1 = 4T / R
iii) Excess of pressure inside air bubble in a liquid.
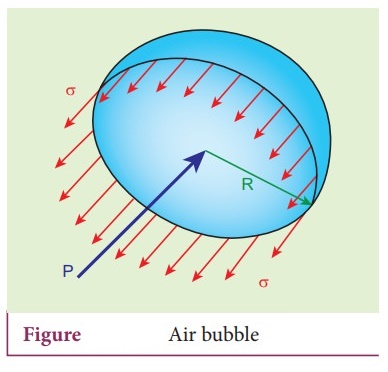
Consider
an air bubble of radius R inside a liquid having surface tension T as shown in
Figure. Let P1 and P2 be the pressure outside and inside the air bubble, respectively. Now, the
excess pressure inside the air bubble is ŌłåP = P1 ŌłÆ P2.
Consider the forces acting on the air bubble are
i)
The force due to surface tension acting towards right around the rim of length 2ŽĆR
is FT = 2ŽĆRT
ii)
The force due to outside pressure P1 is to the right acting across a
cross sectional area of ŽĆR2 is Fp1 = P1 ŽĆR2
iii)
The force due to pressure P2 inside the bubble, acting to the left
is Fp2 = P2 ŽĆR2. As the air bubble is in
equilibrium under the action of these forces, Fp2 = FT +
Fp1
P2
ŽĆR2 = 2ŽĆRT + P1 ŽĆR2
ŌćÆ (P2 - P1)
ŽĆR2 = 2ŽĆRT
Excess
pressure is ŌłåP = P2 ŌłÆ P1 = 2T / R

10. What is capillarity? Obtain an expression for the surface tension of a liquid by capillary rise method.
ŌŚÅ
Consider a capillary tube which is held vertically in a beaker containing
water; the water rises in the capillary tube to a height due to surface
tension.
ŌŚÅ
The surface tension force FT acts along the tangent at the point of
contact downwards and its reaction force upwards.
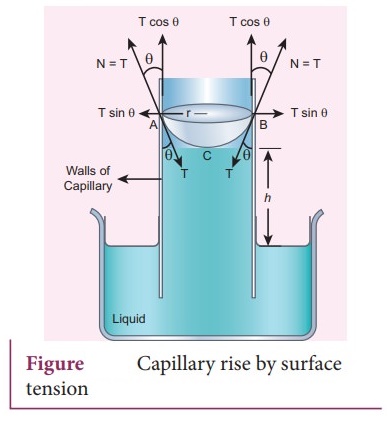
ŌŚÅ
Surface tension T, is resolved into two components i) Horizontal component T
sin ╬Ė and
ii)
Vertical component T cos ╬Ė acting upwards, all along the whole circumference of
the meniscus.
ŌŚÅ
Total upward force = (T cos ╬Ė)( 2ŽĆr) = 2ŽĆr T cos ╬Ė
ŌŚÅ
Where ╬Ė is the angle of contact; r is the radius of the tube.
ŌŚÅ Let p be the density of water and h be the height to which the liquid rises inside the tube. Then,
(the volume of liquid column in the tube, V ) = (volume of the liquid column of radius r height h ) + (volume of liquid of radius r and height r-volume of the hemisphere of radius r )

V
= ŽĆr2h + (ŽĆr2├Śr ŌĆō 2/3 ŽĆr3
)
ŌćÆ V = ŽĆr2h + 1/3 ŽĆr3
ŌŚÅ
The upward force supports the weight of the liquid column above the free
surface.
ŌŚÅ
Therefore,
2ŽĆrT
cos╬Ė = ŽĆr2 ( h+1/3r) Žüg
ŌćÆ T = [ r(h +
1/3 r) Žüg ] / 2cos╬Ė
ŌŚÅ
If the capillary is a very fine tube of radius (i.e., radius is very small)
then r/3 can be neglected when it is compared to the height h.
ŌŚÅ
Therefore, T = rŽügh / 2cos╬Ė
h = 2T cos╬Ė
/ rŽüg
ŌćÆ h ╬▒ 1/r
ŌŚÅ
h is inversely proportional to the radius (r) of the tube. The smaller the radius
of the tube greater will be the capillarity.
11. Obtain an equation of continuity for a flow of fluid on the basis of conservation of mass.
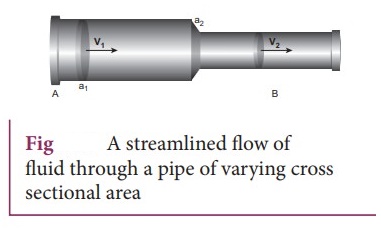
ŌŚÅ
Consider a pipe AB of varying cross sectional area a1 and a2
such that a1 > a2 .
ŌŚÅ
A non-viscous and incompressible liquid flows steadily through the pipe, with
velocities v1 and v2 in area a1 and a2
respectively.
ŌŚÅ
Let m1 be the mass of fluid flowing through section A in time Ōłåt, m1
= (a1v1 Ōłåt)Žü
ŌŚÅ
Let m2 be the mass of fluid flowing through section B in time Ōłåt, m2
= (a2v2 Ōłåt)Žü . For an incompressible liquid, mass is
conserved m1 = m2
a1v1
ŌłåtŽü = a2v2 Ōłåt Žü
a1v1
= a2v2
=>
a v = constant
ŌŚÅ
It is called the equation of continuity and it is a statement of conservation
of mass in the flow of fluids.ŌĆā
ŌŚÅ
In general, a v = constant, which means that the volume flux or flow rate
remains constant throughout the pipe. In other words, the smaller the cross
section, greater will be the velocity of the fluid.
12. State and prove BernoulliŌĆÖs theorem for a flow of incompressible, non-viscous, and streamlined flow of fluid.
Bernoulli's
theorem:
According
to Bernoulli's theorem, the sum of pressure energy, kinetic energy, and
potential energy per unit mass of an incompressible, non-viscous fluid in a
streamlined flow remains a constant.
P/Žü + 1/2 v2 + gh = constant, this is known as Bernoulli's equation.
Proof:
ŌŚÅ
Let us consider a flow of liquid through a pipe AB as shown in Figure.
ŌŚÅ
Let v be the volume of the liquid when it enters A in a time t which is equal
to the volume of the liquid leaving B in the same time.
ŌŚÅ
Let aA, vA and PA be the area of cross section
of the tube, velocity of the liquid and pressure exerted by the liquid at A
respectively.
ŌŚÅ
Let the force exerted by the liquid at A is FA= PAaA
ŌŚÅ
Distance travelled by the liquid in time t is d = vA t
Therefore,
the work done is W = FAd = PAaA vA
t
But,
aAvA t = aAd = V, volume of the liquid
entering at A.
Thus,
the work done is the pressure energy (at A), W = FAd = PAV
Pressure
energy per unit volume at A = Pressure energy / Volume = PAV
/ V = PA
Pressure
energy per unit mass at A = Pressure energy / Mass = PAV
/ m = PA / [m /V ] = PA
/ Žü
Since
m is the mass of the liquid entering at A in a given time, therefore, pressure
energy of the liquid at A is
EPA = PAV
= PAV ├Ś (m / m) = m [PA / Žü]
Potential
energy of the liquid at A, PEA = mg hA,
Due
to the flow of liquid, the kinetic energy of the liquid at A,
KEA
= 1/2 mv2A
Therefore,
the total energy due to the flow of liquid at A,
EA
= EPA + KEA + PEA
EA =m
PA/Žü + 1/2 mv2A + mghA
Similarly,
let aB, vB, and PB be the area of cross
section of the tube, velocity of the liquid, and pressure exerted by the liquid
at B. Calculating the total energy at EB, we get
EB
= m PB/Žü + 1/2 mv2B + mg hB
From
the law of conservation of energy, EA = EB
m PA/Žü + 1/2 mv2A + mghA = m PB/Žü + 1/2 mv2B + mg hB
PA/Žü
+ 1/2 v2A + ghA = PB/Žü + 1/2 v2B
+ g hB = constant
Thus,
the above equation can be written as
P/Žüg + 1/2 v2/g + h = constant
13. Describe the construction and working of venturimeter and obtain an equation for the volume of liquid flowing per second through a wider entry of the tube.
Venturimeter.
ŌŚÅ
This device is used to measure the rate of flow (or say flow speed) of the incompressible
fluid flowing through a pipe. It works on the principle of Bernoulli's theorem.
ŌŚÅ
Let P1 be the pressure of the fluid at the wider region of the tube
A.
ŌŚÅ
The fluid of density 'Žü' flows from the pipe with speed 'v1' and
into the narrow region, its speed increases to 'v2'
ŌŚÅ
According to the Bernoulli's equation, this increase in speed is accompanied by
a decreases in the fluid pressure P2 at the narrow region of the
tube B.
ŌŚÅ
Therefore, the pressure difference between the tubes A and B is noted by
measuring the height difference (ŌłåP=P1ŌłÆP2) between the
surfaces of the monometer liquid.
ŌŚÅ
From the equation of continuity, Av1 = a v2
v2
= [ A/a ] v1
ŌŚÅ
Using Bernoulli's equation, P1 + Žü (v12/
2) = P2 + Žü(v22/2) = P2
+ Žü 1/2( (A / a)
v1)2
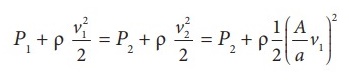
ŌŚÅ
From the above equation, the pressure difference, ΔP = P1
- P2 = Žü v12/ 2 ( [A2
ŌĆō a2] / a2 )
ŌŚÅ
Thus, the speed of flow of fluid at the wide end of the tube A

ŌŚÅ
The volume of the liquid flowing out per second is
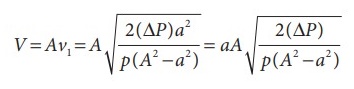
Related Topics