Surface Tension by capillary rise method

Surface Tension by capillary rise method

The pressure difference across a curved liquid-air interface is the basic factor behind the rising up of water in a narrow tube (influence of gravity is ignored). The capillary rise is more dominant in the case of very fine tubes. But this phenomenon is the outcome of the force of surface tension. 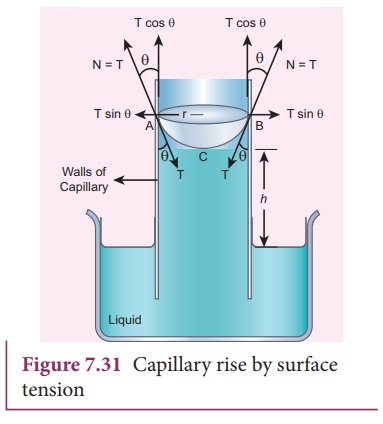In order to arrive a relation between the capillary rise (h) and surface tension (T), consider a capillary tube which is held vertically in a beaker containing water; the water rises in the capillary tube to a height h due to surface tension (Figure 7.31).

The surface tension force F_T, acts along the tangent at the point of contact downwards and its reaction force upwards. Surface tension T, is resolved into two components i)  Horizontal component T sinθ and ii)  Vertical component T cosθ acting upwards, all along the whole circumference of the meniscus.

Total upward force

= (T cosθ) (2πr) = 2πrT cosθ

where θ is the angle of contact, r is the radius of the tube. Let ρ be the density of water and h be the height to which the liquid rises inside the tube. Then,

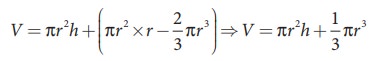
The upward force supports the weight of the liquid column above the free surface,

therefore,

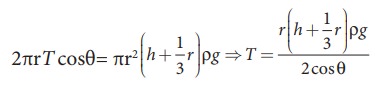
If the capillary is a very fine tube of radius (i.e., radius is very small) then r/3 can be neglected when it is compared to the height h. Therefore,

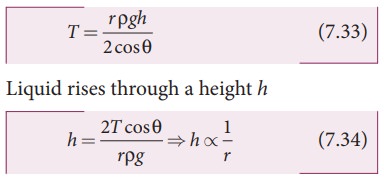
This implies that the capillary rise (h) is inversely proportional to the radius (r) of the tube. i.e, the smaller the radius of the tube greater will be the capillarity.

EXAMPLE 7.12

Water rises in a capillary tube to a height of 2.0cm. How much will the water rise through another capillary tube whose radius is one-third of the first tube?

Solution

From equation (7.34), we have

h ∝ 1/r ⇒hr =constant

Consider two capillary tubes with radius r₁ and r₂ which on placing in a liquid, capillary rises to height h₁ and h₂, respectively. Then,

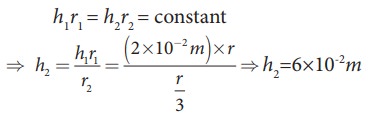
EXAMPLE 7.13

Mercury has an angle of contact equal to 140° with soda lime glass. A narrow tube of radius 2 mm, made of this glass is dipped in a trough containing mercury. By what amount does the mercury dip down in the tube relative to the liquid surface outside?. Surface tension of mercury T=0.456 N m^-1; Density of mercury ρ = 13.6 × 103 kg m-3

Solution

Capillary descent,

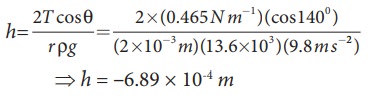
where, negative sign indicates that there is fall of mercury (mercury is depressed) in glass tube.