Chapter: 11th Physics : UNIT 7 : Properties of Matter
Solved Example Problems for Moduli of elasticity
There are three types of elastic modulus.
![]()
![]() (a) Young’s modulus
(a) Young’s modulus
(b) Rigidity modulus (or Shear modulus)
(c) Bulk modulus
EXAMPLE 7.1
Within the elastic limit, the stretching strain produced in wires A, B, and C due to stress is shown in the figure. Assume the load applied are the same and discuss the elastic property of the material.
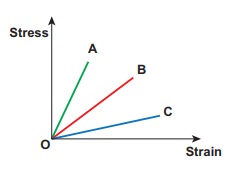
Write down the elastic modulus in ascending order.
Solution
Here, the elastic modulus is Young modulus and due to stretching, stress is tensile stress and strain is tensile strain.
Within the elastic limit, stress is proportional to strain (obey Hooke’s law). Therefore, it shows a straight line behavior. So, the modulus of elasticity (here, Young modulus) can be computed by taking slope from this straight line. Hence, calculating the slope for the straight line, we get
Slope of A > Slope of B > Slope of C
Which implies,
Young modulus of C < Young modulus of B < Young modulus of A
Notice that larger the slope, lesser the strain (fractional change in length). So, the material is much stiffer. Hence, the elasticity of wire A is greater than wire B which is greater than C. From this example, we have understood that Young’s modulus measures the resistance of solid to a change in its length.
EXAMPLE 7.2
A wire 10 m long has a cross-sectional area 1.25 x 10-4 m2. It is subjected to a load of 5 kg. If Young’s modulus of the material is 4 x 1010 N m-2, calculate the elongation produced in the wire.
Take g = 10 ms-2.
Solution
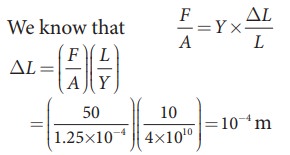
(b) Rigidity modulus (or Shear modulus)
EXAMPLE 7.3
A metallic cube of side 100 cm is subjected to a uniform force acting normal to the whole surface of the cube. The pressure is 106 pascal. If the volume changes by 1.5 x 10-5 m3, calculate the bulk modulus of the material.
Solution
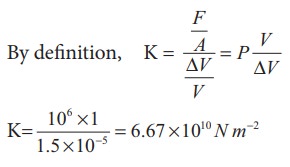
EXAMPLE 7.4
A metal cube of side 0.20 m is subjected to a shearing force of 4000 N. The top surface is displaced through 0.50 cm with respect to the bottom. Calculate the shear modulus of elasticity of the metal.
Solution
Here, L = 0.20 m, F = 4000 N, x = 0.50 cm
= 0.005 m and Area A = L2 = 0.04 m2
Therefore, Shear modulus
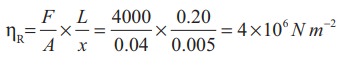
Related Topics