Properties of Matter - Equation of continuity | 11th Physics : UNIT 7 : Properties of Matter
Chapter: 11th Physics : UNIT 7 : Properties of Matter
Equation of continuity
Equation of continuity
In order to discuss the mass flow rate through a pipe, it is necessary to assume that the flow of fluid is steady, the flow of the fluid is said to be steady if at any given point, the velocity of each passing fluid particle remains constant with respect to time. Under this condition, the path taken by the fluid particle is a streamline.
Consider a pipe AB of varying cross sectional area a1 and a2 such that a1 > a2. A non-viscous and incompressible liquid flows steadily through the pipe, with velocities v1 and v2 in area a1 and a2, respectively as shown in Figure 7.32.
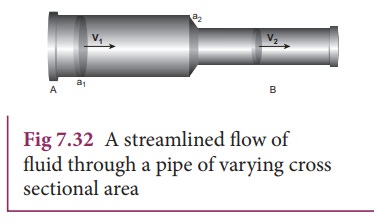
Let m1 be the mass of fluid flowing through section A in time ╬öt, m1 = (a1v1 t) Žü
Let m2 be the mass of fluid flowing through section B in time t, m2 = (a2v2 t) Žü
For an incompressible liquid, mass is conserved m1 = m2
a1 v1 ╬öt Žü = a2 v2 ╬öt Žü
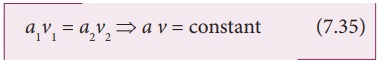
which is called the equation of continuity and it is a statement of conservation of mass in the flow of fluids.
In general, a v = constant, which means that the volume flux or flow rate remains constant throughout the pipe. In other words, the smaller the cross section, greater will be the velocity of the fluid.
EXAMPLE 7.14
In a normal adult, the average speed of the blood through the aorta (radius r = 0.8 cm) is 0.33 ms-1. From the aorta, the blood goes into major arteries, which are 30 in number, each of radius 0.4 cm. Calculate the speed of the blood through the arteries.
Solution:
a1v1 = 30 a2 v2 ŌćÆ ŽĆ r12v1 = 30 ŽĆ r22v2
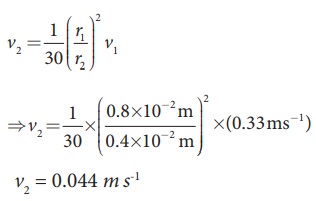
Related Topics