Stress and strain

Stress and strain

(a) Stress:

When a force is applied, the size or shape or both may change due to the change in relative positions of atoms or molecules. This deformation may not be noticeable to our naked eyes but it exists in the material itself. When a body is subjected to such a deforming force, internal force is developed in it, called as restoring force. The force per unit area is called as stress.

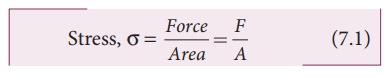
The SI unit of stress is N m^-2 or pascal (Pa) and its dimension is [ML^-1T^-2]. Stress is a tensor.

(i) Longitudinal stress and shearing stress:

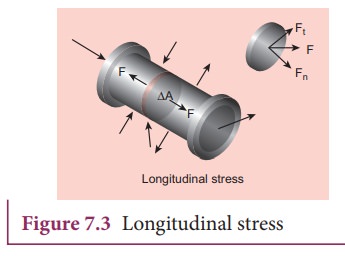
Let us consider a body as shown in Figure 7.3. When many forces act on the system (body), the center of mass (defined in unit 5) remains at rest. However, the body gets deformed due to these forces and so the internal forces appear. Let ∆A be the cross sectional area of the body. The parts of the body on the two sides of ∆A exert internal forces and − on each other which is due to deformation. The force can be resolved in two components, F_n normal to the surface ∆A (perpendicular to the surface) and F_t tangential to the surface ∆A (tangent to the surface). The normal stress or longitudinal stress (σ_n) over the area is defined as

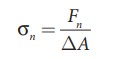
Similarly, the tangential stress or shearing stress σ_t over the area is defined as

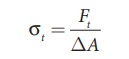
Longitudinal stress can be classified into two types, tensile stress and compressive stress.

Tensile stress

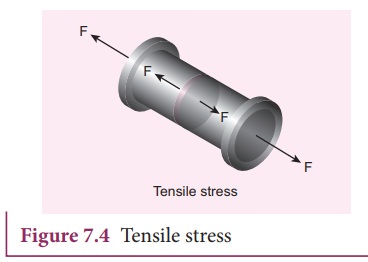
Internal forces on the two sides of ∆A may pull each other, i.e., it is stretched by equal and opposite forces. Then, the longitudinal stress is called tensile stress.

Compressive stress

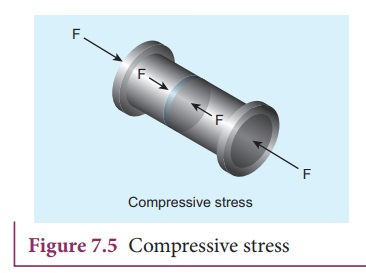
When forces acting on the two sides of ∆A push each other, ∆A is pushed by equal and opposite forces at the two ends. In this case, ∆A is said to be under compression. Then, the longitudinal stress is called compressive stress.

(ii) Volume stress

This happens when a body is acted by forces everywhere on the surface such that the force at any point is normal to the surface and the magnitude of the force on a small surface area is proportional to the area. For instance, when a solid is immersed in a fluid, the pressure at the location of the solid is P, the force on any area ∆A is

F = P ∆A

Where, F is perpendicular to the area. Thus, force per unit area is called volume stress.

which is the same as the pressure.

(b) Strain:

Strain measures how much an object is stretched or deformed when a force is applied. Strain deals with the fractional change in the size of the object, in other words, strain measures the degree of deformation. As an example, in one dimension, consider a rod of length l when it stretches to a new length ∆l then

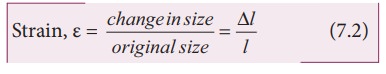
 Îµ is a dimensionless quantity and has no unit. Strain is classified into three types.

(1)  Longitudinal strain

When a rod of length l is pulled by equal and opposite forces, the longitudinal strain is defined as

Longitudinal strain can be classified into two types

(i) Tensile strain: If the length is increased from its natural length then it is known as tensile strain.

(ii) Compressive strain: If the length is decreased from its natural length then it is known as compressive strain.

(2)  Shearing strain

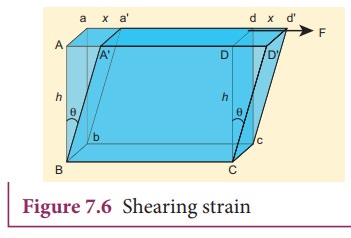
Consider a cuboid as shown in Figure 7.6. Let us assume that the body remains in translational and rotational equilibrium. Let us apply the tangential force F along AD such that the cuboid deforms as shown in Figure 7.6. Hence, shearing strain or shear is (ε_s)

For small angle, tanθ ≈ θ

Therefore, shearing strain or shear,

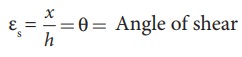
(3)  Volume strain

If the body is subjected to a volume stress, the volume will change. Let V be the original volume of the body before stress and V + ∆V be the change in volume due to stress. The volume strain which measures the fractional change in volume is

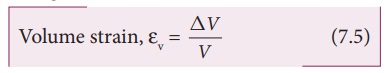
Elastic Limit

The maximum stress within which the body regains its original size and shape after the removal of deforming force is called the elastic limit.

If the deforming force exceeds the elastic limit, the body acquires a permanent deformation. For example, rubber band loses its elasticity if pulled apart too much. It changes its size and becomes misfit to be used again.