Chapter: 11th Physics : UNIT 7 : Properties of Matter
Surface energy (S.E.) and surface tension (S.T.)
Surface
energy (S.E.) and surface tension (S.T.)
Surface Energy
Consider
a sample of liquid in a container. A molecule inside the liquid is being pulled
in all direction by other molecules that surround it. However, near the
surface, a molecule is pulled down only by the molecules below them and there
is a net downward force. As a result, the entire surface of the liquid is being
pulled inward. The liquid surface thus tends to have the least surface area. To
increase the surface area, some molecules are brought from the interior to the
surface. For this reason, work has to be done against the forces of attraction.
The amount of work done is stored as potential energy. Thus, the molecules
lying on the surface possess greater potential energy than other molecules.
This excess energy per unit area of the free surface of the liquid is called ŌĆśsurface energyŌĆÖ. In other words, the
work done in increasing the surface area per unit area of the liquid against
the surface tension force is called the surface energy of the liquid.

It
is expressed in JŌĆåm-2 or NŌĆåm-1 .
Surface tension
The
surface tension of a liquid is defined as the energy per unit area of the
surface of a liquid

The SI unit and dimensions of T are N mŌłÆ1 and M TŌłÆ2,
respectively.
Relation between surface tension and surface energy:
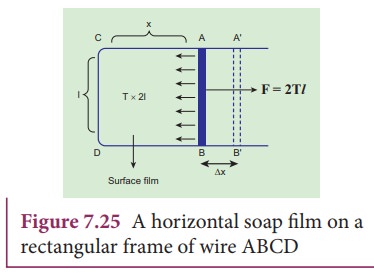
Consider
a rectangular frame of wire ABCD in a soap solution (Figure 7.25). Let AB be
the movable wire. Suppose the frame is dipped in soap solution, soap film is
formed which pulls the wire AB inward due to surface tension. Let F be the force due to surface tension,
then
F = (2T)l
here,
2 is introduced because it has two free surfaces. Suppose AB is moved by a
small distance Ōłåx to new a position A'B'.
Since the area increases, some work has to be done against the inward force due
to surface tension.
Work
done = Force ├Ś distance = (2T l) (╬öx)
Increase
in area of the film ŌłåA = (2l)
(Δx)=2l x
Therefore,

Hence,
the surface energy per unit area of a surface is numerically equal to the
surface tension.
EXAMPLE 7.10
Let
2 .4├Ś10ŌłÆ4 J
of work is done to increase the area of a film of soap bubble from 50 cm2 to
100 cm2. Calculate the value of surface tension of soap solution.
Solution:
A
soap bubble has two free surfaces, therefore increase in surface area ŌłåA = A2ŌłÆA1 = 2(100-50) ├Ś 10-4m2 = 100 ├Ś 10-4m2.
Since,
work done W = T ├Ś╬öA ŌćÆT =
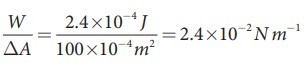
Related Topics