Chapter: 11th Physics : UNIT 7 : Properties of Matter
Excess of pressure inside a liquid drop, a soap bubble, and an air bubble
Excess
of pressure inside a liquid drop, a soap bubble, and an air bubble
As
it is discussed earlier, the free surface of a liquid becomes curved when it
has contact with a solid. Depending upon the nature of liquid-air or liquid-gas
interface, the magnitude of interfacial surface tension varies. In other words,
as a consequence of surface tension, the above such interfaces have energy and
for a given volume, the surface will have a minimum energy with least area. Due
to this reason, the liquid drop becomes spherical (for a smaller radius).
When
the free surface of the liquid is curved, there is a difference in pressure
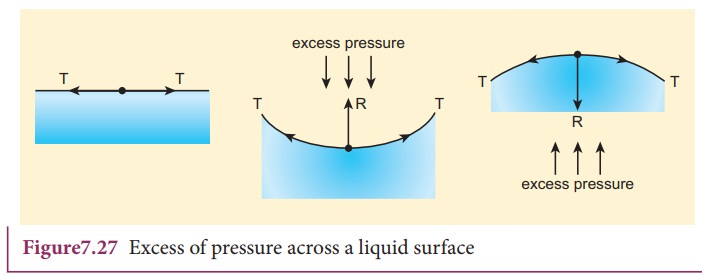
between the inner and outer the side of the surface (Figure 7.27).
i) When the liquid surface is plane, the forces due to surface tension (T, T) act tangentially to the liquid surface in opposite directions. Hence, the resultant force on the molecule is zero. Therefore, in the case of a plane liquid surface, the pressure on the liquid side is equal to the pressure on the vapour side.
ii)
When the liquid surface is curved, every molecule on the liquid surface
experiences forces (FT, FT) due to surface tension
along the tangent to the surface. Resolving these forces into rectangular
components, we find that horizontal components cancel out each other while
vertical components get added up. Therefore, the resultant force normal to the
surface acts on the curved surface of the liquid. Similarly, for a convex
surface, the resultant force is directed inwards towards the centre of
curvature, whereas the resultant force is directed outwards from the centre of
curvature for a concave surface. Thus, for a curved liquid surface in
equilibrium, the pressure on its concave side is greater than the pressure on
its convex side.
Excess of pressure inside a bubble and a liquid drop:
The
small bubbles and liquid drops are spherical because of the forces of surface
tension. The fact that a bubble or a liquid drop does not collapse due to the
combined effect indicates that the pressure inside a bubble or a drop is
greater than that outside it.
1) Excess of pressure inside air bubble in a liquid.
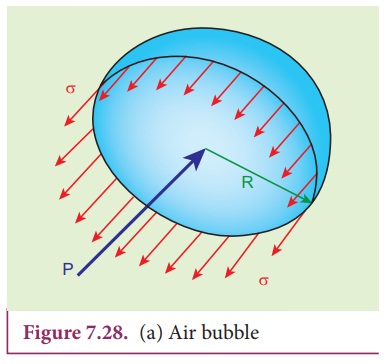
Consider
an air bubble of radius R inside a liquid having surface tension T as shown in
Figure 7.28 (a). Let P1 and P2 be the pressures outside
and inside the air bubble, respectively. Now, the excess pressure inside the
air bubble is ΔP = P1 − P2.
In
order to find the excess pressure inside the air bubble, let us consider the
forces acting on the air bubble. For the hemispherical portion of the bubble,
considering the forces acting on it, we get,
i) The
force due to surface tension acting towards right around the rim of length 2Ï€R
is FT = 2Ï€RT
ii)
The force due to outside pressure P1
is to the right acting across a cross sectional area of πR2 is FP1=
P1Ï€R2
iii)
The force due to pressure P2
inside the bubble, acting to the left is FP2=
P2Ï€R2.
As
the air bubble is in equilibrium under the action of these forces, FP2= FT + FP1
P2Ï€R2 = 2Ï€RT
+ P1Ï€R2
(P2 − P1)πR2
= 2Ï€RT
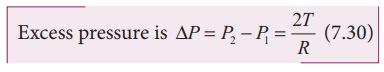
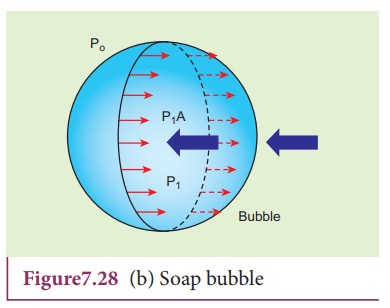
2) Excess pressure inside a soap bubble
Consider a soap bubble of radius R and the surface tension of the soap bubble be T as shown in Figure 7.28 (b). A soap
bubble has two liquid surfaces in contact with air, one inside the bubble and
other outside the bubble. Therefore, the force on the soap bubble due to
surface tension is 2×2πRT. The
various forces acting on the soap bubble are,
i)
Force due to surface tension FT=4Ï€RT towards right
ii)
Force due to outside pressure, FP1=
P1Ï€R2 towards right
iii)
Force due to inside pressure, FP2=
P2Ï€R2 towards left
As
the bubble is in equilibrium, FP2=
FT + FP1
P2Ï€R2 = 4Ï€RT
+ P1Ï€R2
(P2 − P1)πR2
= 4Ï€RT
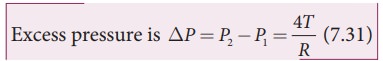
3) Excess pressure inside the liquid drop
Consider
a liquid drop of radius R and the surface tension of the liquid is T as shown
in Figure 7.28 (c).
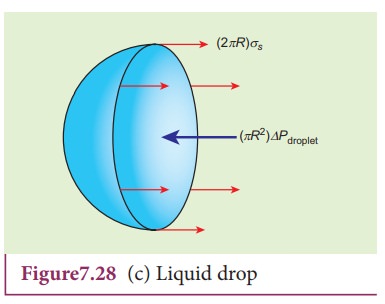
The
various forces acting on the liquid drop are,
i)
Force due to surface tension FT=2Ï€RT towards right
ii)
Force due to outside pressure, FP1=
P1Ï€R2 towards right
iii)
Force due to inside pressure, FP2=
P2Ï€R2 towards left
As
the drop is in equilibrium,
FP2= FT + FP1
P2Ï€R2 = 2Ï€RT
+ P1Ï€R2
=
> (P2 − P1)πR2 = 2πRT
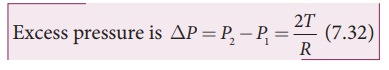
EXAMPLE 7.11
If
excess pressure is balanced by a column of oil (with specific gravity 0.8) 4 mm high, where R = 2.0 cm, find the surface tension of the soap
bubble.
Solution
The
excess of pressure inside the soap
T = 15.68 ×10− 2 N m−1
Related Topics