Properties of Matter - PoissonŌĆÖs ratio | 11th Physics : UNIT 7 : Properties of Matter
Chapter: 11th Physics : UNIT 7 : Properties of Matter
PoissonŌĆÖs ratio
PoissonŌĆÖs
ratio

Suppose
we stretch a wire, its length increases (elongation) but its diameter decreases
(contraction). Similarly, when we stretch a rubber band (elongation), it
becomes noticeably thinner (contraction). That is, deformation of the material
in one direction produces deformation in another direction. To quantify this,
French Physicist S.D. Poisson proposed a ratio, known as PoissonŌĆÖs ratio, which
is defined as the ratio of relative contraction (lateral strain) to relative
expansion (longitudinal strain). It is denoted by the symbol ┬Ą.

For
a wire of length L with diameter D, due to applied force, wire stretches
and hence, increase in length be l
and decrease in diameter be d, then

Negative
sign indicates the elongation along longitudinal and contraction along lateral
dimension. Further, notice that it is the ratio between quantities of the same
dimension. So, PoissonŌĆÖs ratio has no unit and no dimension (dimensionless
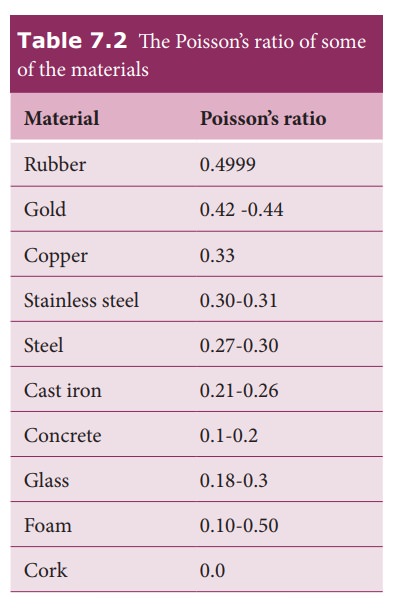
number). The PoissonŌĆÖs ratio values of some of the materials are listed in
Table 7.2.
Related Topics