Chapter: 11th Physics : UNIT 7 : Properties of Matter
Pressure due to fluid column at rest
Pressure
due to fluid column at rest
A
mountaineer climbing the mountain is able to experience a decrease in pressure
with altitude. A person jumping into the swimming pool always realizes an
increase in pressure with depth below the water surface. In both the cases, the
pressure encountered by the mountaineer and diver is usually due to the
hydrostatic pressure, because they are due to fluids that are static. In order
to understand the increase in pressure with depth below the water surface,
consider a water sample of cross sectional area in the form of a cylinder. Let h1 and h2 be the depths from the air-water interface to level 1
and level 2 of the cylinder, respectively as shown in Figure 7.10(a). Let F1
be the force acting downwards on level 1 and F2 be the force acting
upwards on level 2, such that, F1 = P1 A and F2
= P2 A Let us assume the mass of the sample to be m and under equilibrium condition, the
total upward force (F2) is balanced by the total downward force (F1
+ mg), in other words, the gravitational force will act downward which is being
exactly balanced by the difference between the force F2 ŌĆō F1.
F2 ŌĆō F1= mg =
FG (7.15)

where
m is the mass of the water available
in the sample element. Let Žü be the density of the water then,
the mass of water available in the sample element is

Hence,
gravitational force,
FG
= Žü A (h2 ŌĆō h1) g
On
substituting the value of W in equation (7.15)
F2=F1+m g ŌćÆ P2A = P1A+ ŽüA(h2-h1)g
Cancelling
out A on both sides,
P2 = P1 + Žü(h2
ŌĆō h1)g (7.16)

If
we choose the level 1 at the surface of the liquid (i.e., air-water interface)
and the level 2 at a depth ŌĆśhŌĆÖ below the surface (as shown in Figure 7.10(b)),
then the value of h1 becomes zero (h1 = 0) and in turn P1
assumes the value of atmospheric pressure (say Pa). In addition, the
pressure (P2) at a depth becomes P. Substituting these values in
equation (7.16), we get
P = Pa + Žügh (7.17)

which
means, the pressure at a depth h is greater than the pressure on the surface of
the liquid, where Pa is the atmospheric pressure which is equal to
1.013 x 105 Pa.
If
the atmospheric pressure is neglected or ignored then
P = Žügh (7.18)

For
a given liquid, Žü is fixed and g is also constant, then the pressure due to the
fluid column is directly proportional to vertical distance or height of the
fluid column. This implies, the height of the fluid column is more important to
decide the pressure and not the cross sectional or base area or even the shape
of the container.
When
we talk about liquid at rest, the liquid pressure is the same at all points at
the same horizontal level (or same depth). This statement can be demonstrated
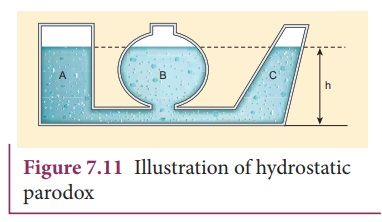
by an experiment called ŌĆśhydrostatic paradoxŌĆÖ. Let us consider three vessels of
different shapes A, B, and C as shown in Figure 7.11. These vessels are
connected at the bottom by a horizontal pipe. When they are filled with a
liquid (say water), it occupies the same level even though the vessels hold
different amounts of water. It is true because the liquid at the bottom of each
section of the vessel experiences the same pressure.
Related Topics