Poisson’s ratio

Poisson’s ratio

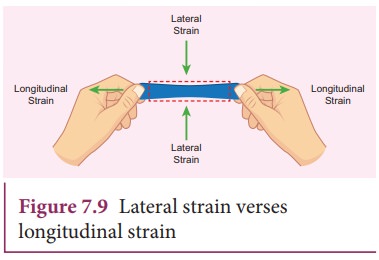
Suppose we stretch a wire, its length increases (elongation) but its diameter decreases (contraction). Similarly, when we stretch a rubber band (elongation), it becomes noticeably thinner (contraction). That is, deformation of the material in one direction produces deformation in another direction. To quantify this, French Physicist S.D. Poisson proposed a ratio, known as Poisson’s ratio, which is defined as the ratio of relative contraction (lateral strain) to relative expansion (longitudinal strain). It is denoted by the symbol µ.

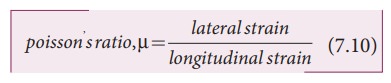
For a wire of length L with diameter D, due to applied force, wire stretches and hence, increase in length be l and decrease in diameter be d, then

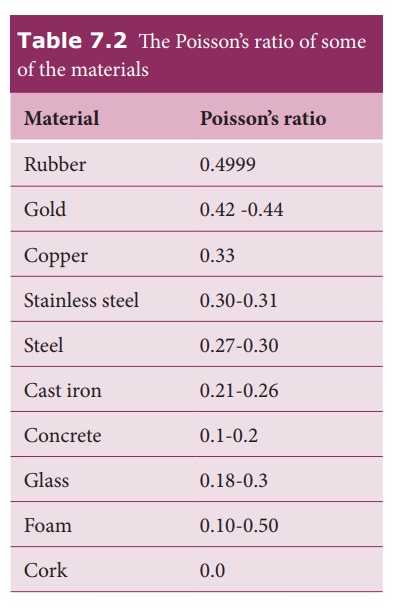
Negative sign indicates the elongation along longitudinal and contraction along lateral dimension. Further, notice that it is the ratio between quantities of the same dimension. So, Poisson’s ratio has no unit and no dimension (dimensionless number). The Poisson’s ratio values of some of the materials are listed in Table 7.2.