Poiseuille’s equation

Poiseuille’s equation

Poiseuille analyzed the steady flow of liquid through a capillary tube. He derived an expression for the volume of the liquid flowing per second through the capillary tube.

As per the theory, the following conditions must be retained while deriving the equation.

·           The flow of liquid through the tube is streamlined.

·           The tube is horizontal so that gravity does not influence the flow

·           The layer in contact with the wall of the tube is at rest

·           The pressure is uniform over any cross section of the tube

We can derive Poiseuille’s equation using dimensional analysis. Consider a liquid flowing steadily through a horizontal capillary tube. Let v=(V/t) be the volume of  the liquid flowing out per second through a capillary tube. It depends on (1) coefficient of viscosity (η) of the liquid, (2) radius of the tube (r), and (3) the pressure gradient (P/l) .

Then,

where, k is a dimensionless constant. Therefore,

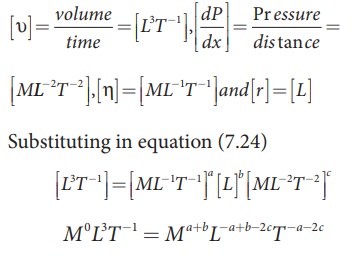
So, equating the powers of M, L, and T on both sides, we get

a + c = 0, −a + b âˆ’2c =3, and −a âˆ’2c = −1

We have three unknowns a, b, and c. We have three equations, on solving, we get

a = −1, b = 4, and c = 1

Therefore, equation (7.24) becomes,

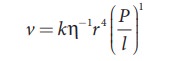
Experimentally, the value of k is shown to be π/8 , we have

The above equation is known as Poiseuille’s equation for the flow of liquid through a narrow tube or a capillary tube. This relation holds good for the fluids whose velocities are lesser than the critical velocity (vc).