Jacobi’s Identity and Lagrange’s Identity

Jacobi’s Identity and Lagrange’s Identity

Theorem 6.9 (Jacobi’s identity)

For any three vectors , , , we have  = .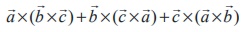

Proof

Using vector triple product expansion, we have

Adding the above equations and using the scalar product of two vectors is commutative, we get

.

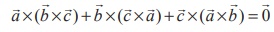Theorem 6.10 (Lagrange’s identity)

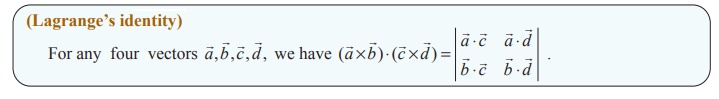
Proof

Since dot and cross can be interchanged in a scalar product, we get

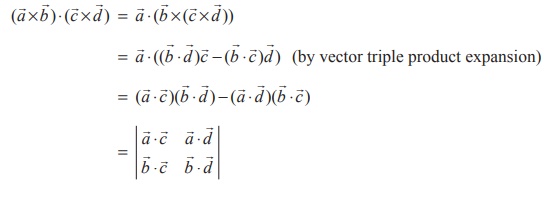
Example 6.19

Prove that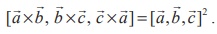 

Solution

Using the definition of the scalar triple product, we get

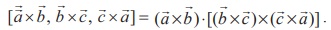                        ..............(1)

By treating (× ) as the first vector in the vector triple product, we find

Using this value in (1), we get

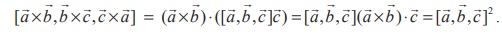
Example 6.20

Prove that .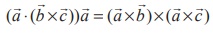

Solution

Treating ( Ã—  ) as the first vector on the right hand side of the given equation and using the vector triple product expansion, we get

Example 6.21

For any four vectors , , , , we have

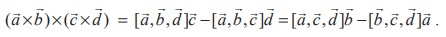
Solution

Taking = ( Ã—  )  as a single vector and  using the vector triple product expansion, we get

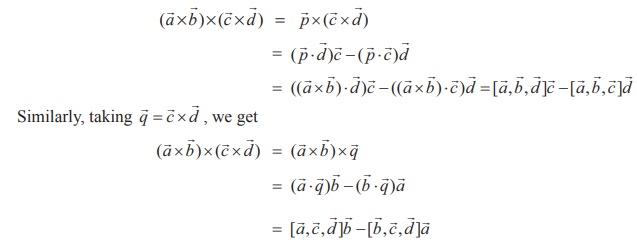
Example 6.22

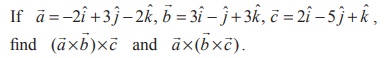
State whether they are equal.

Solution

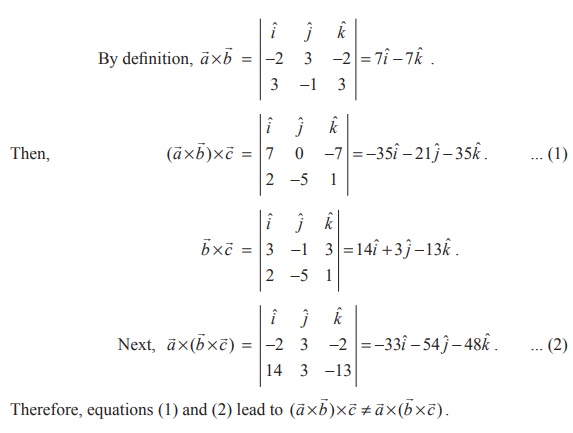
Example 6.23

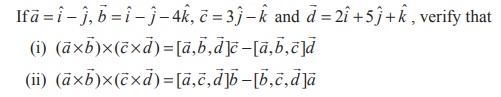
Solution (i)

By definition,

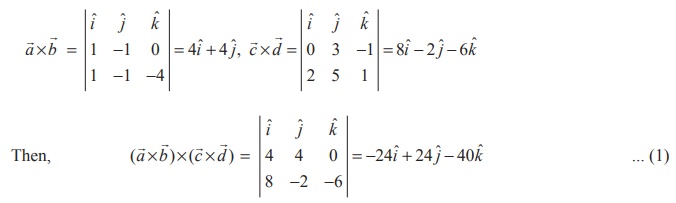
On the other hand, we have

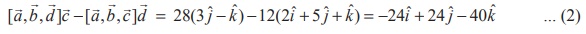
Therefore, from equations (1) and (2), identity (i) is verified.

The verification of identity (ii) is left as an exercise to the reader.