Chapter: 12th Mathematics : UNIT 6 : Applications of Vector Algebra
Image of a Point in a Plane
Image
of a Point in a Plane
Let A be the given point whose position vector is ![]() .
Let
.
Let ![]() ⋅
⋅ ![]() = p be the equation
of the plane.
= p be the equation
of the plane.
Let ![]() be the position vector of the mirror
image A′ of A in the plane. Then
be the position vector of the mirror
image A′ of A in the plane. Then ![]() is
perpendicular to the plane. So it is parallel to
is
perpendicular to the plane. So it is parallel to ![]() . Then
. Then
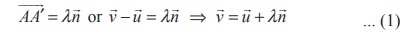
Let M be the middle point of AA′. Then the position vector of M
is ![]() . But M lies on the plane.
. But M lies on the plane.
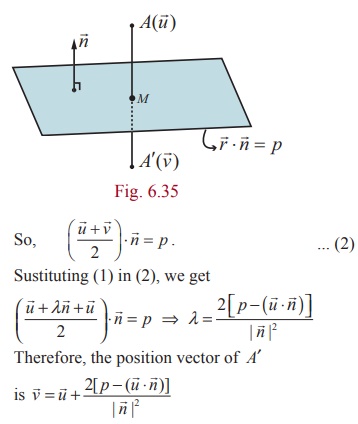
Note
The mid point of M
of AA′ is the foot of the
perpendicular from the point A to the
plane ![]() .
.![]() = p.
= p.
So the position vector of the foot M of the perpendicular is given by .
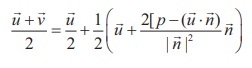
The coordinates of the image of a point in a plane
Let (a1,
a2, a 3) be the point ![]() whose
image in the plane is required. Then
whose
image in the plane is required. Then ![]() = a1ˆi + a2ˆj + a3ˆk
= a1ˆi + a2ˆj + a3ˆk
Let ax + by + cz = d be the equation
of the given plane. Writing the equation in the vector form we get ![]() .
.![]() = p where
= p where ![]() = aˆi + bˆj
+ cˆk Then the position vector of the image is
= aˆi + bˆj
+ cˆk Then the position vector of the image is
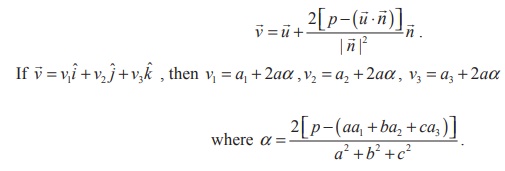
Example 6.55
Find the image of the point whose position vector is ˆi + 2ˆj + 3ˆk in
the plane ![]() ⋅ (ˆi + 2ˆj + 4ˆk ) = 38 .
⋅ (ˆi + 2ˆj + 4ˆk ) = 38 .
Solution
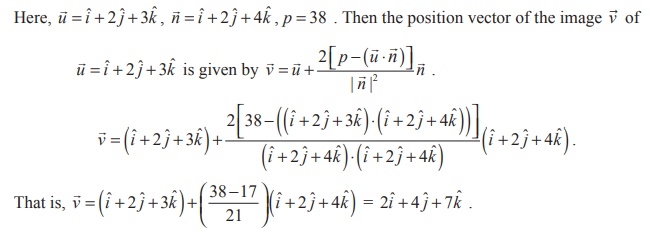
Therefore, the image of
the point with position vector iˆ + 2
ˆj + 3kˆ is 2iˆ + 4 ˆj + 7kˆ
.
Note
The foot of the
perpendicular from the point with position vector iˆ + 2ˆj + 3kˆ in the given plane is
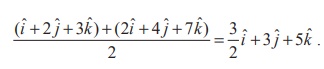
Related Topics