Hooke’s law and its experimental verification

Hooke’s law and its experimental verification

Hooke’s law is for a small deformation, when the stress and strain are proportional to each other. It can be verified in a simple way by stretching a thin straight wire (stretches like spring) of length L and uniform cross-sectional area A suspended from a fixed point O. A pan and a pointer are attached at the free end of the wire as shown in Figure 7.7 (a). The extension produced on the wire is measured using a vernier scale arrangement. The experiment shows that for a given load, the corresponding stretching force is F and the elongation produced on the wire is ΔL. It is directly proportional to the original length L and inversely proportional to the area of cross section A. A graph is plotted using F on the X- axis and ΔL on the Y- axis. This graph is a straight line passing through the origin as shown in Figure 7.7 (b).

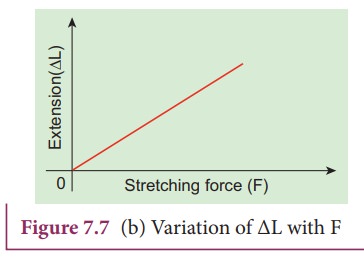
Therefore,

∆L = (slope)F

Multiplying and dividing by volume,

V = A L,

Comparing with equation (7.1) and equation (7.2), we get equation (7.5) as

σ ∝ ε

i.e., the stress is proportional to the strain in the elastic limit.

Stress – Strain profile curve:

The stress versus strain profile is a plot in which stress and strain are noted for each load and a graph is drawn taking strain along the X-axis and stress along the Y-axis. The elastic characteristics of the materials can be analyzed from the stress-strain profile.

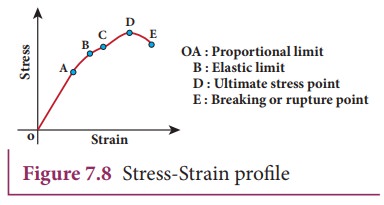
(a) Portion OA:

In this region, stress is very small such that stress is proportional to strain, which means Hooke’s law is valid. The point A is called limit of proportionality because above this point Hooke’s law is not valid. The slope of the line OA gives the Young’s modulus of the wire.

(b) Portion AB:

This region is reached if the stress is increased by a very small amount. In this region, stress is not proportional to the strain. But once the stretching force is removed, the wire will regain its original length. This behaviour ends at point B and hence, the point B is known as yield point (elastic limit). The elastic behaviour of the material (here wire) in stress-strain curve is OAB.

(c) Portion BC:

If the wire is stretched beyond the point B (elastic limit), stress increases and the wire will not regain its original length after the removal of stretching force.

(d) Portion CD:

With further increase in stress (beyond the point C), the strain increases rapidly and reaches the point D. Beyond D, the strain increases even when the load is removed and breaks (ruptures) at the point E. Therefore, the maximum stress (here D) beyond which the wire breaks is called breaking stress or tensile strength. The corresponding point D is known as fracture point. The region BCDE represents the plastic behaviour of the material of the wire.