Problem Questions with Answer, Solution - Exercise 6.9: Equation of intersection of the planes | 12th Mathematics : UNIT 6 : Applications of Vector Algebra
Chapter: 12th Mathematics : UNIT 6 : Applications of Vector Algebra
Exercise 6.9: Equation of intersection of the planes
EXERCISE 6.9
1. Find the equation of the plane passing through the line of intersection of the planes ![]() = (2ˆi - 7ˆj + 4ˆk ) = 3 and 3x - 5 y + 4z +11 = 0 , and the point (-2,1, 3) .
= (2ˆi - 7ˆj + 4ˆk ) = 3 and 3x - 5 y + 4z +11 = 0 , and the point (-2,1, 3) .

2. Find the equation of the plane passing through the line of intersection of the planes x + 2 y + 3z = 2 and x - y + z +11 = 3 , and at a distance 2/√3 from the point (3,1, -1).
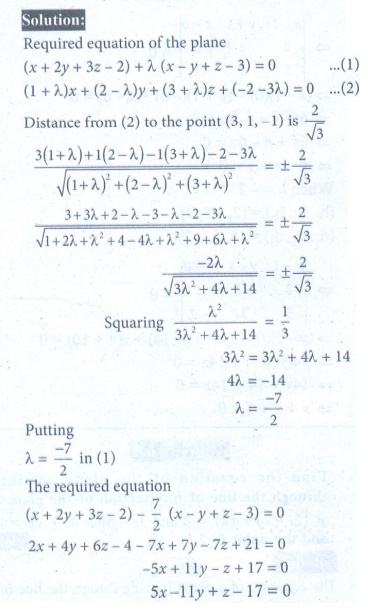
3. Find the angle between the line ![]() = (2ˆi - ˆj + ˆk )+t(ˆi + 2ˆj - ˆk) and the plane
= (2ˆi - ˆj + ˆk )+t(ˆi + 2ˆj - ˆk) and the plane ![]() . (6ˆi + 3ˆj + 2ˆk ) = 8
. (6ˆi + 3ˆj + 2ˆk ) = 8

4. Find the angle between the planes ![]() = (ˆi + ˆj - 2ˆk ) = 3 and 2x - 2 y + z = 2 .
= (ˆi + ˆj - 2ˆk ) = 3 and 2x - 2 y + z = 2 .

5. Find the equation of the plane which passes through the point (3, 4, -1) and is parallel to the plane 2x - 3y + 5z + 7 = 0 . Also, find the distance between the two planes.

6. Find the length of the perpendicular from the point (1, -2, 3) to the plane x - y + z = 5 .
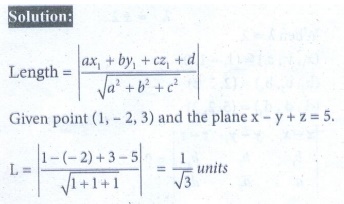
7. Find the point of intersection of the line x -1 = y/2 = z +1 with the plane 2x - y + 2z = 2 . Also, find the angle between the line and the plane.

8. Find the coordinates of the foot of the perpendicular and length of the perpendicular from the point ( 4,3,2) to the plane x + 2 y + 3z = 2 .

Answers:
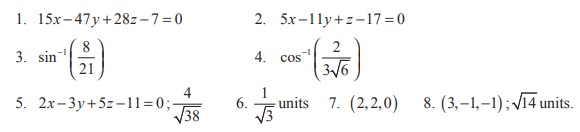
Related Topics