Chapter: 12th Mathematics : UNIT 6 : Applications of Vector Algebra
Equation of plane containing two non-parallel coplanar lines
Equation
of plane containing two non-parallel coplanar lines
(a) Parametric form of vector equation
Let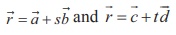 
be two non-parallel coplanar lines.
Then 
× 
≠
. Let P be any point on the plane
and let 
0 be its position vector. Then, the
vectors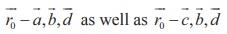 
are also coplanar. So, we get 
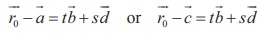. Hence, the vector equation in parametric form is 
.
(b) Non-parametric form of vector equation
Let 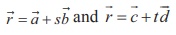be two non-parallel coplanar lines. Then × ≠. Let P be any point on the plane and let 0 be
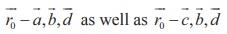its position vector. Then, the vectors are
also coplanar. So, we get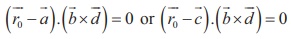 
. Hence, the vector equation in non-parametric form is 
.
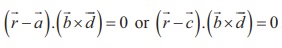(C) Cartesian form of equation of plane
In Cartesian form the equation of the plane containing the two
given coplanar lines
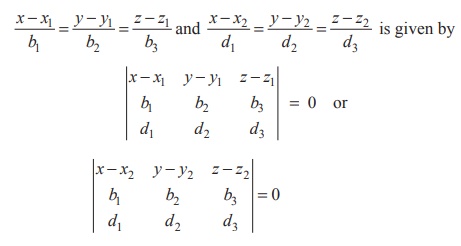
Example 6.46
Show that the lines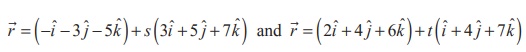 
are coplanar. Also,find the non-parametric form of vector
equation of the plane containing these lines.
Solution
Comparing the two given lines with
We know that the two given lines are coplanar ,
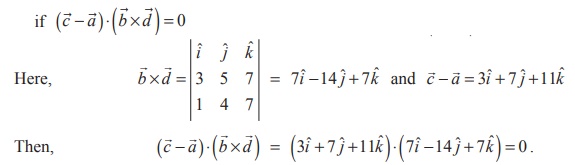
Therefore the two given lines are coplanar.Then we find the non
parametric form of vector equation of the plane containing the two given
coplanar lines. We know that the plane containing the two given coplanar lines
is
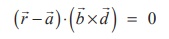
which implies that ( - (-iˆ - 3ˆj - 5kˆ)).(7iˆ -14ˆj + 7kˆ) = 0 . Thus, the
required non-parametric vector equation of the plane containing the two given
coplanar lines is . (iˆ - 2ˆj
+ ˆk ) = 0.
Related Topics