Distance between two parallel planes

Distance between two parallel planes

Theorem 6.21

The distance between two parallel planes ax + by + cz + d₁ = 0 and ax + by + cz + d₂ = 0 is given by 

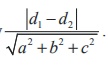
Proof

Let A( x₁ , y₁ , z₁ ) be any point on the plane ax + by + cz + d₂ = 0 , then we have

ax₁ + by₁ + cz₁ + d₂ = 0 ⇒ ax₁ + by₁ + cz₁ = −d₂

The distance of the plane ax + by + cz + d₁ = 0 from the point A( x₁ , y₁ , z₁ ) is given by

Hence, the distance between two parallel planes ax + by + cz + d₁ = 0 and ax + by + cz + d₂ = 0 given by δ = .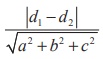

Example 6.51

Find the distance between the parallel planes x + 2 y − 2z +1 = 0 and 2x + 4 y − 4z + 5 = 0

Solution

We know that the formula for the distance between two parallel planes ax + by + cz + d₁ = 0 and ax + by + cz + d₂ = 0 is 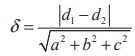 Rewrite the second equation as x + 2y – 2z + 5/2 = 0. Comparing the given equations with the general equations, we get a = 1, b = 2, c = −2, d₁=1, d₂ = 5/2.

Substituting these values in the formula, we get the distance

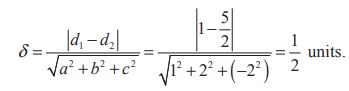
Example 6.52

Find the distance between the planes â‹…

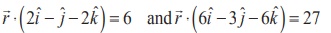
Solution

Let  be the position vector of an arbitrary point on the plane â‹…(2 ˆi − ˆj − 2 ˆk ) = 6 . Then, we have

â‹…(2 Ë†i âˆ’ ˆj âˆ’ 2 Ë†k ) = 6                           .................(1)

If δ is the distance between the given planes, then δ is the perpendicular distance from  to the plane