Equation, its applications - BernoulliŌĆÖs Theorem | 11th Physics : UNIT 7 : Properties of Matter
Chapter: 11th Physics : UNIT 7 : Properties of Matter
BernoulliŌĆÖs Theorem
BERNOULLIŌĆÖS
THEOREM
Equation of continuity
In
order to discuss the mass flow rate through a pipe, it is necessary to assume
that the flow of fluid is steady, the flow of the fluid is said to be steady if
at any given point, the velocity of each passing fluid particle remains
constant with respect to time. Under this condition, the path taken by the fluid
particle is a streamline.
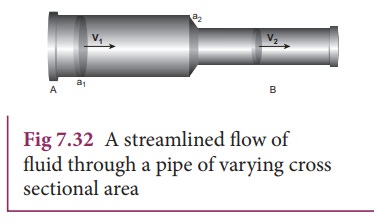
Consider
a pipe AB of varying cross sectional area a1
and a2 such that a1 > a2. A non-viscous and incompressible liquid flows
steadily through the pipe, with velocities v1 and
v2 in area a1 and a2,
respectively as shown in Figure 7.32.
Let
m1 be the mass of fluid flowing through section A in time Δt, m1
= (a1v1 t) Žü
Let
m2 be the mass of fluid flowing through section B in time t, m2
= (a2v2 t) Žü
For
an incompressible liquid, mass is conserved m1 = m2
a1
v1 ╬öt Žü = a2 v2 ╬öt Žü
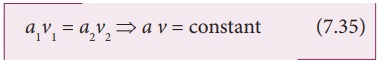
which
is called the equation of continuity and it is a statement of conservation of
mass in the flow of fluids.
In
general, a v = constant, which means
that the volume flux or flow rate remains constant throughout the pipe. In
other words, the smaller the cross section, greater will be the velocity of the
fluid.
EXAMPLE 7.14
In
a normal adult, the average speed of the blood through the aorta (radius r = 0.8 cm) is 0.33 ms-1.
From the aorta, the blood goes into
major arteries, which are 30 in number, each of radius 0.4 cm. Calculate the speed of the blood through the arteries.
Solution:
a1v1 = 30 a2 v2 ŌćÆ ŽĆ r12v1 = 30 ŽĆ r22v2
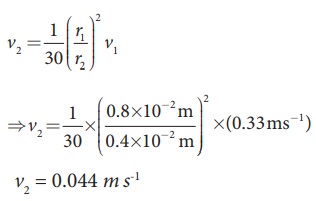
Pressure, kinetic and potential energy of liquids
A
liquid in a steady flow can possess three kinds of energy. They are (1) Kinetic
energy, (2) Potential energy, and (3) Pressure energy, respectively.
i) Kinetic energy:ŌĆé The kinetic energy of a liquid of mass m moving with a velocity v is
given by

The
kinetic energy per unit mass =
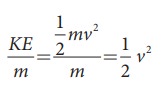
Similarly,
the kinetic energy per unit volume
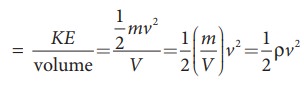
ii)
Potential energy: The potential
energy of a liquid of mass m at a
height h above the ground level is
given by
PE =
mgh
The
potential energy per unit mass
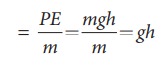
Similarly,
the potential energy per unit volume =
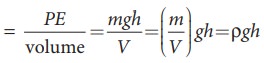
ii) Pressure energy: The energy acquired by a fluid by applying pressure on the
fluid. We know that
Pressure
= Force/Area ŌćÆ
Force = Pressure ├Ś Area
F
├Ś d = (P A) ├Ś d = P (A ├Ś d)
F
├Ś d = W = P V = pressure energy
Therefore,
pressure energy, EP = PV The pressure energy per unit mass =
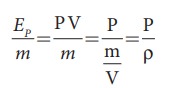
Similarly, the
potential energy per
unit volume =
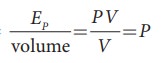
BernoulliŌĆÖs theorem and its applications
In
1738, the Swiss scientist Daniel Bernoulli developed a relationship for the
flow of fluid through a pipe of varying cross section. He proposed a theorem
for the streamline flow of a liquid based on the law of conservation of energy.
BernoulliŌĆÖs theorem
According to BernoulliŌĆÖs theorem, the sum of pressure energy, kinetic energy, and potential energy per unit mass of an incompressible, non-viscous fluid in a streamlined flow remains a constant. Mathematically,
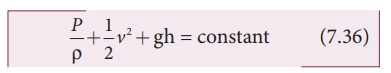
This
is known as BernoulliŌĆÖs equation.
Proof:
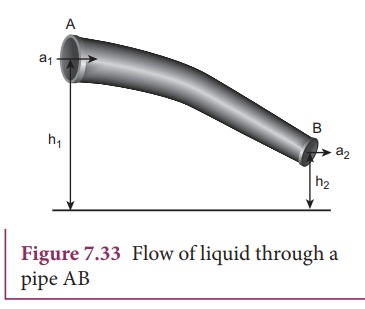
Let
us consider a flow of liquid through a pipe AB as shown in Figure 7.33. Let V be the volume of the liquid when it
enters A in a time t which is equal to the volume of the
liquid leaving B in the same time.
Let aA, vA and PA be the area of cross section of the tube, velocity of the liquid and pressure exerted by the
liquid at A respectively.
Let
the force exerted by the liquid at A
is
FA =
PAaA
Distance
travelled by the liquid in time t is
d = vA t
Therefore,
the work done is
W = FAd = PAaAvA t
But
aAvAt = aAd =V, volume of the liquid entering at A.
Thus,
the work done is the pressure energy (at A),ŌĆā
W = FAd
= PAV
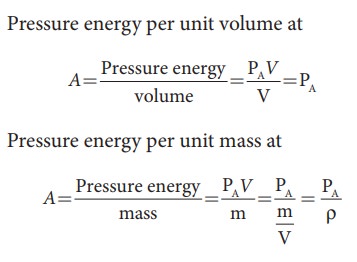
Since
m is the mass of the liquid entering at A in a given time, therefore, pressure
energy of the liquid at A is
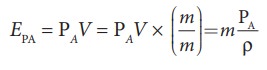
Potential
energy of the liquid at A,
PEA = mg hA,
Due
to the flow of liquid, the kinetic energy of the liquid at A,
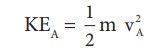
Therefore, the total energy due to the flow of liquid at A, EA = EPA + KEA + PEA
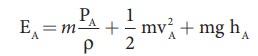
Similarly,
let aB, vB, and PB be the
area of cross section of the tube, velocity of the liquid, and pressure exerted
by the liquid at B. Calculating the
total energy at EB, we get
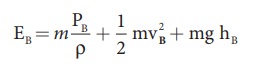
From
the law of conservation of energy,
EA
= EB
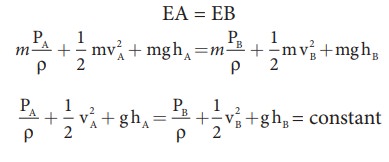
Thus,
the above equation can be written as
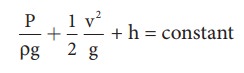
The
above equation is the consequence of the conservation of energy which is true
until there is no loss of energy due to friction. But in practice, some energy
is lost due to friction. This arises due to the fact that in a fluid flow, the
layers flowing with different velocities exert frictional forces on each other.
This loss of energy is generally converted into heat energy. Therefore,
BernoulliŌĆÖs relation is strictly valid for fluids with zero viscosity or
non-viscous liquids. Notice that when the liquid flows through a horizontal
pipe, then h = 0
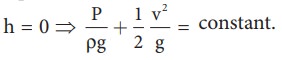
Applications of BernoulliŌĆÖs Theorem
(a) Blowing off roofs during wind
storm In olden
days, the roofs of the huts or houses were designed with a slope as shown in
Figure.7.34. One important scientific reason is that as per the BernoulliŌĆÖs
principle, it will be safeguarded except roof during storm or cyclone.
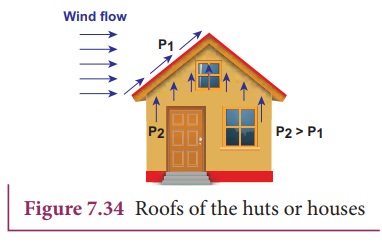
During cyclonic condition, the roof is blown off without damaging the other parts of the house. In accordance with the BernoulliŌĆÖs principle, the high wind blowing over the roof creates a low-pressure P1. The pressure under the roof P2 is greater. Therefore, this pressure difference (P2ŌĆōP1) creates an up thrust and the roof is blown off.
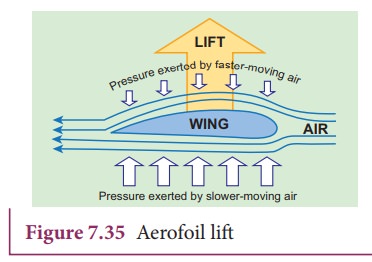
(b) Aerofoil lift
The
wings of an airplane (aerofoil) are so designed that its upper surface is more
curved than the lower surface and the front edge is broader than the real edge.
As the aircraft moves, the air moves faster above the aerofoil than at the
bottom as shown in Figure 7.35.
According
to BernoulliŌĆÖs Principle, the pressure of air below is greater than above,
which creates an upthrust called the dynamic lift to the aircraft.
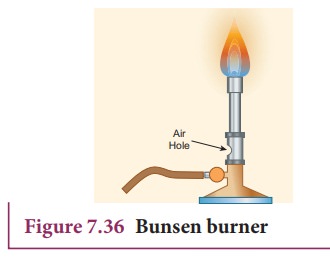
(c) Bunsen burner
In
this, the gas comes out of the nozzle with high velocity, hence the pressure in
the stem decreases. So outside air reaches into the burner through an air vent
and the mixture of air and gas gives a blue flame as shown in Figure 7.36.
(d) Venturimeter
This
device is used to measure the rate of flow (or say flow speed) of the
incompressible fluid flowing through a pipe. It works on the principle of
BernoulliŌĆÖs theorem. It consists of two wider tubes A and A' (with cross
sectional area A) connected by a narrow tube B (with cross sectional area a). A manometer in the form of U-tube is
also attached between the wide and narrow tubes as shown in Figure7.37. The
manometer contains a liquid of density ŌĆśŽümŌĆÖ.
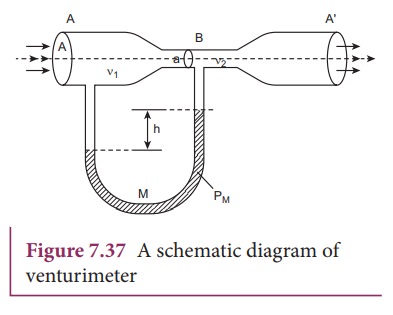
Let
P1 be the pressure of the
fluid at the wider region of the tube A. Let us assume that the fluid of
density ŌĆśŽüŌĆÖ flows from the pipe with speed ŌĆśv1ŌĆÖ
and into the narrow region, its speed increases to ŌĆśv2ŌĆÖ. According to the BernoulliŌĆÖs equation, this
increase in speed is accompanied by a decrease in the fluid pressure P2 at the narrow region of
the tube B. Therefore, the pressure difference between the tubes A and B is
noted by measuring the height difference (ΔP
= P1ŌłÆP2) between the surfaces of the manometer liquid.
From
the equation of continuity, we can say that Av1 = a v2
which means that
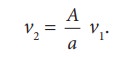
Using
BernoulliŌĆÖs equation,
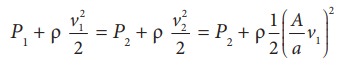
From
the above equation, the pressure difference

Thus,
the speed of flow of fluid at the wide end of the tube A
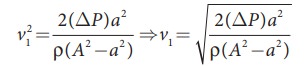
The
volume of the liquid flowing out per second is
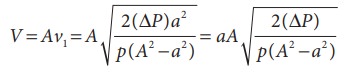
(e) Other applications
This BernoulliŌĆÖs concept is mainly used in the design of carburetor of automobiles, filter pumps, atomizers, and sprayers.
For example,
the carburetor has a very fine channel called nozzle through which the air is
allowed to flow in larger speed. In this case, the pressure is lowered at the
narrow neck and in turn, the required fuel or petrol is sucked into the chamber
so as to provide the correct mixture of air and fuel necessary for ignition
process.
Related Topics