Chapter: 11th Physics : UNIT 7 : Properties of Matter
Applications of BernoulliŌĆÖs Theorem
Applications of BernoulliŌĆÖs Theorem
(a) Blowing off roofs during wind storm
In olden days, the roofs of the huts or houses were designed with a slope as shown in Figure.7.34. One important scientific reason is that as per the BernoulliŌĆÖs principle, it will be safeguarded except roof during storm or cyclone.
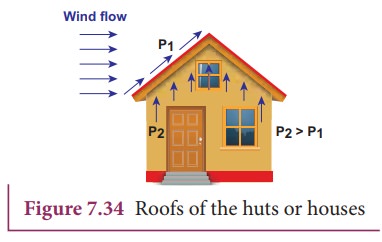
During cyclonic condition, the roof is blown off without damaging the other parts of the house. In accordance with the BernoulliŌĆÖs principle, the high wind blowing over the roof creates a low-pressure P1. The pressure under the roof P2 is greater. Therefore, this pressure difference (P2ŌĆōP1) creates an up thrust and the roof is blown off.
(b) Aerofoil lift
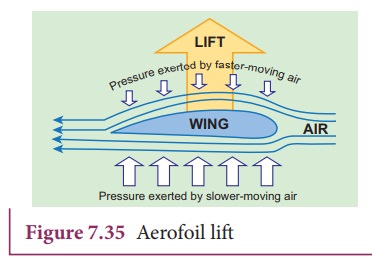
The wings of an airplane (aerofoil) are so designed that its upper surface is more curved than the lower surface and the front edge is broader than the real edge. As the aircraft moves, the air moves faster above the aerofoil than at the bottom as shown in Figure 7.35.
According to BernoulliŌĆÖs Principle, the pressure of air below is greater than above, which creates an upthrust called the dynamic lift to the aircraft.
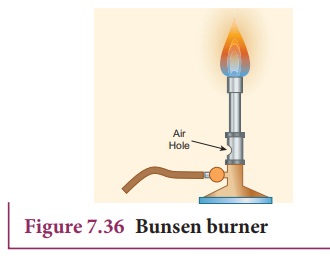
(c) Bunsen burner
In this, the gas comes out of the nozzle with high velocity, hence the pressure in the stem decreases. So outside air reaches into the burner through an air vent and the mixture of air and gas gives a blue flame as shown in Figure 7.36.
(d) Venturimeter
This device is used to measure the rate of flow (or say flow speed) of the incompressible fluid flowing through a pipe. It works on the principle of BernoulliŌĆÖs theorem. It consists of two wider tubes A and A' (with cross sectional area A) connected by a narrow tube B (with cross sectional area a). A manometer in the form of U-tube is also attached between the wide and narrow tubes as shown in Figure7.37. The manometer contains a liquid of density ŌĆśŽümŌĆÖ.
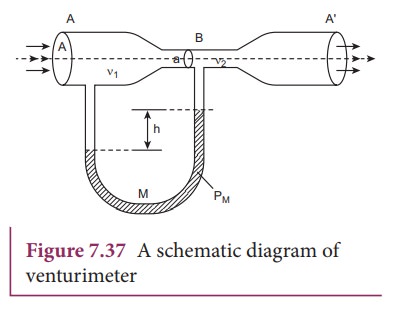
Let P1 be the pressure of the fluid at the wider region of the tube A. Let us assume that the fluid of density ŌĆśŽüŌĆÖ flows from the pipe with speed ŌĆśv1ŌĆÖ and into the narrow region, its speed increases to ŌĆśv2ŌĆÖ. According to the BernoulliŌĆÖs equation, this increase in speed is accompanied by a decrease in the fluid pressure P2 at the narrow region of the tube B. Therefore, the pressure difference between the tubes A and B is noted by measuring the height difference (╬öP = P1ŌłÆP2) between the surfaces of the manometer liquid.
From the equation of continuity, we can say that Av1 = a v2 which means that
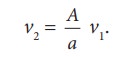
Using BernoulliŌĆÖs equation,
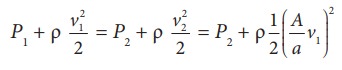
From the above equation, the pressure difference
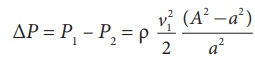
Thus, the speed of flow of fluid at the wide end of the tube A
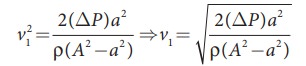
The volume of the liquid flowing out per second is
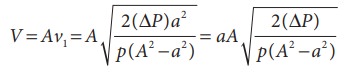
(e) Other applications
This BernoulliŌĆÖs concept is mainly used in the design of carburetor of automobiles, filter pumps, atomizers, and sprayers.
For example, the carburetor has a very fine channel called nozzle through which the air is allowed to flow in larger speed. In this case, the pressure is lowered at the narrow neck and in turn, the required fuel or petrol is sucked into the chamber so as to provide the correct mixture of air and fuel necessary for ignition process.
Related Topics