Exercises problems with Solution | Physics - Solved Example Problem for Physics: Kinematics | 11th Physics : UNIT 2 : Kinematics
Chapter: 11th Physics : UNIT 2 : Kinematics
Solved Example Problem for Physics: Kinematics
Exercises
1. The position vectors particle has length 1m and makes 30° with the x-axis. What are the lengths of the x and y components of the position vector?




6. An object at an angle such that the horizontal range is 4 times of the maximum height. What is the angle of projection of the object?
[Ans: θ = 45°]

7. The following graphs represent velocity – time graph. Identify what kind of motion a particle undergoes in each graph.

Answers:
(a) (i) It represents the uniform acceleration.
Body starts from nest and move with constant velocity
(ii) Greater is the slope v – (1/N)t graph, greater will be the acceleration.
(b) Body moving with uniform velocity, zero slope indicates zero acceleration.
(c) Straight line v (1/N)t graph does not pass the origin. After some time it moves with a uniform acceleration, [acceleration is constant but greater than first graph]
(d) Greater changes in velocity are taking place in equal intervals of time. It represents an increasing acceleration ie. acceleration is variable.
8. The following velocity–time graph represents a particle moving in the positive x–direction. Analyse its motion from 0 to 7 s. Calculate the displacement covered and distance travelled by the particle from 0 to 2 s.
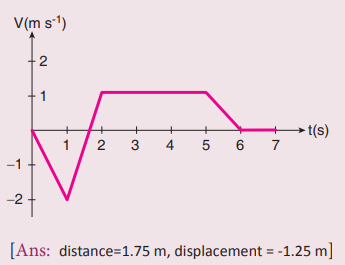
Answers:
It is uniform motion

Distance travelled by the particle
= area of ΔOAB = 1/2 × b × h
OB = b; PA = h
= ½ × 1.5 × 2 = 1.5m
Displacement covered = + ½ × b × h
= ½ × 1.5 × (-2)
A particle moves with -ve velocity along OA, then moves with uniform Velocity and retards uniformly then it comes to rest at E.
9. A particle is projected at an angle of T with respect to the horizontal direction. Match the following for the above motion.
Ans: Position vector – remains downward
Answers:
(a) vx - remains constant
(b) vy - decreases and increases
(c) Acceleration - remains downward
(d) Position vector - varies
[Ans: v x : remains constant ͕ v y : decreases and increases, a remains downward, r: varies]
10. A water fountain on the ground sprinkles water all around it. If the speed of the water coming out of the fountain is v. Calculate the total area around the fountain that gets wet.
Answers:
Speed of the water coming out of the fountion - v
The maximum distance the water wets = Rmax
Total area around the fountain that gets wet = A = ?
A = πR2max.
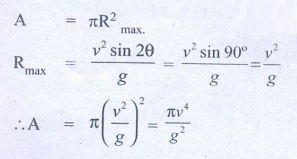
[Ans: Area = πv2/g2]
11. The following table gives the range of a particle when thrown on different planets. All the particles are thrown at the same angle with the horizontal and with the same initial speed. Arrange the planets in ascending order according to their acceleration due to gravity, (g value).
Planet Range
Jupiter 50 m
Earth 75 m
Mars 90 m
Mercury 95 m
Answers:
(Ascending order)
1. Jupiter 50 m – greater ‘g’ value.
2. Earth 75 m
3. Mars 90 m
4. Mercury – Smaller ‘g’ value.
[Ans: g jupiter is greater, gmercury is smaller]
12. The resultant of two vectors A and B is perpendicular to vector A and its magnitude is equal to half of the magnitude of vector B. Then the angle between A and B is
a) 30° b) 45° c) 150° d) 120°
Answers:
Resultant of two vectors A & B = R
Magnitude of R = B/2
Angle between A & B = ?
R = B sin θ => B/2 = B sin θ
Sin θ = (B/2) / B = ½
θ = 30°
The angle between A & B = 180° - 30° = 150°.
[Ans: θ = 150°]
13. Compare the components for the following vector equations
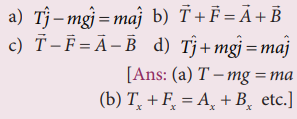
Answer:
(a) T - mg = ma
(b) Tx + Fx = Ax + Bxetc.
(c) Tx -Fx = Ax - Bx etc.
(d) T + mg = ma
14. Calculate the area of the triangle for which two of its sides are given by the vectors
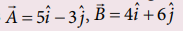
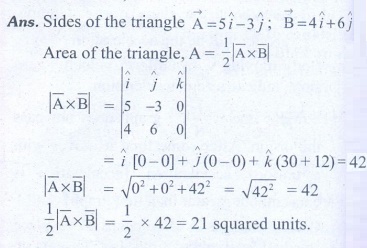
[Ans: Area = 21]
15. If Earth completes one revolution in 24hours, what is the angular displacement made by Earth in one hour. Express your answer in both radian and degree.
Answers:
Time taken for earth to complete one revolution = 24 hr
Angle covered by θ = 360° = 2π radians
For one revolution i.e. 24 hrs, the angular displacement is 2π radians
For one hour, the angular displacement
θ = 2π/24 = π/12
(or)
180°/12 = 15°
θ = π /12 or 15°.
[Ans: θ = 15°or π/12 ]
16. A object is thrown with initial speed 5 ms−1 with an angle of projection 30γ. What is the height and range reached by the particle?

[Ans: height = 0.318 m Range =2.21 m]
17. A foot-ball player hits the ball with speed 20 m s-1 with angle 30° with respect to horizontal direction as shown in the figure. The goal post is at distance of 40 m from him. Find out whether ball reaches the goal post?
Answers:
The speed of the ball, u = 20 m/s.
Angle of projection θ = 30°; g = 9.8 ms-2
Horizontal distance R = ?
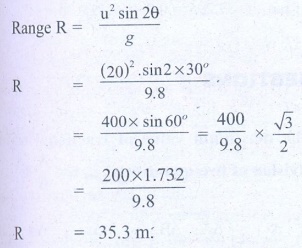
R = 35.3 m.'
The goal post is. at a distance of 40 m , But horizontal distance is 35.3 m. So the ball will not reach the goal post.
[Ans: Ball will not reach the goal post. The range =35.3 m]
18 .If an object is thrown horizontally with an initial speed 10 m s−1 from the top of a building of height 100 m. what is the horizontal distance covered by the particle?
Answer:
h = - 100 m
g = -9.8 m/s2
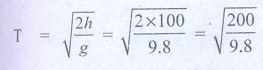
= √(20.408) = 4.51 seconds.
Horizontal distance R = u × T
= 10 × 4.51 =45.1 m.
[Ans: R= 45 m]
19. An object is executing uniform circular motion with an angular speed of π/12 radian per second. At t = 0 the object starts at an angle θ = 0 What is the angular displacement of the particle after 4 s ?

[Ans: 30°]
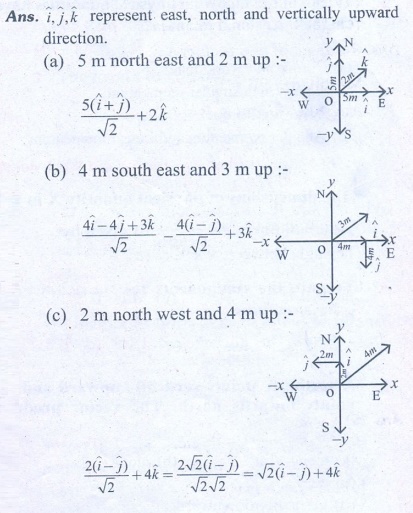
20. Consider the x–axis as representing east, the y–axis as north and z–axis as vertically upwards. Give the vector representing each of the following points.
Ans: 5 m north east and 2 m up

21. The Moon is orbiting the Earth approximately once in 27 days, what is the angle transversed by the Moon per day?
Answer:
Duration taken by the moon in orbiting the earth = 27 days (approx)
The angle transversed by moon per day = 360/27 = 13°3’
[Ans: 13°3’]
22. An object of mass m has angular acceleration α = 0.2rad s−2. What is the angular displacement covered by the object after 3 second? (Assume that the object started with angle zero with zero angular velocity).
Answer:
Angular acceleration α = 0.2 rad s-2
The angular displacement covered by the object after 3 seconds is,

1 rad = 57.295°= 0.9 × 57.295°
θ = 51°
[Ans: 0.9 rad or 51°]
SOLVED EXAMPLE
1. A gun is fired from a place which is at distance 1.2 km from a hill. The echo of the sound is heard back at the same place of firing after 8 second. Find the speed of sound.
Solution:
The echo will be heard when the sound reaches back at the place of firing. So, the total distance travelled by sound is 2 × 1.2 km = 2.4 km = 2400 m.
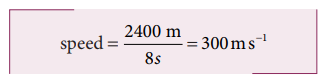
2. A train 100 m long is moving with a speed of 60 kmh-1. In how many seconds will it cross a bridge of 1 km long?
Solution:
Total distance to be covered = 1 km + 100 m = 1100 m (including both bridge and time)
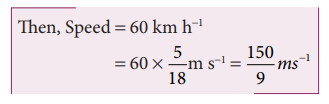
Then, Time taken to cover this
distance = 1100 / (150/9) s = 66 s
3.

4.

5.
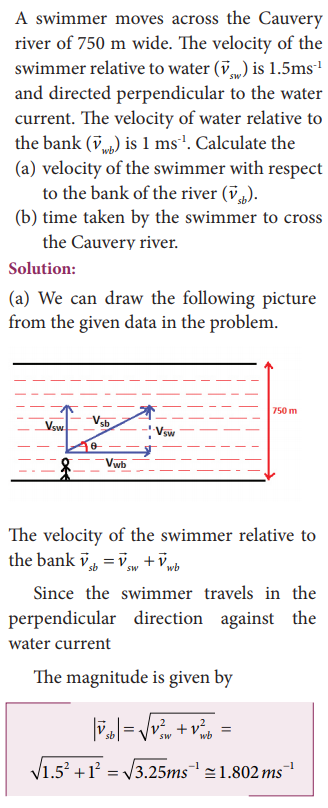
The direction of the swimmer relative to the bank is given by

6. A monkey hangs on a tree. A hunter aims a gun at the monkey and fires the bullet with velocity v0 which makes angle α0 with horizontal direction. At the instant gun fires, monkey leaves the branch and falls straight down to escape from the bullet as shown in the figure. Will bullet hit the monkey or will the monkey escape the bullet? (ignore air resistance)
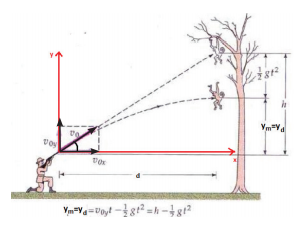
Solution:
As soon as the monkey begins to fall, it will have downward vertical motion with acceleration due to gravity g.
Its equation of motion at any time t is given by
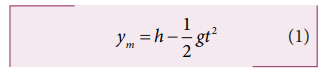
When the bullet comes out of the gun, it has both vertical and horizontal components of velocity given by
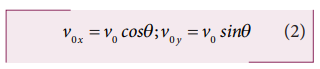
Let us assume the horizontal distance between the monkey and hunter is ‘d’.
At time t, the horizontal distance travelled by the bullet x=v0x , t = v0cosθ
When the horizontal position of bullet, x = d, the time d = v0xT . It implies that T = d / v0 x
At this time T, the vertical distance covered by the bullet is

By substituting this in the equation (3), we get,
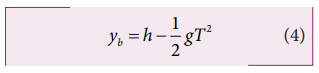
At this same time T, the vertical position of the monkey can be calculated from the equation (1)
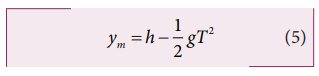
Note that at the time T, the y coordinate of both monkey and bullet is same. It implies that the bullet will hit the monkey.
7. A three storey building of height 100m is located on Earth and a similar building is also located on Moon. If two people jump from the top of these buildings on Earth and Moon simultaneously, when will they reach the ground and at what speed? (g = 10 m s-2)
Solution:

The person on earth reaches ground with greater velocity than the person on the moon
8. The following graphs represent position – time graphs. Arrange the graphs in ascending order of increasing speed.
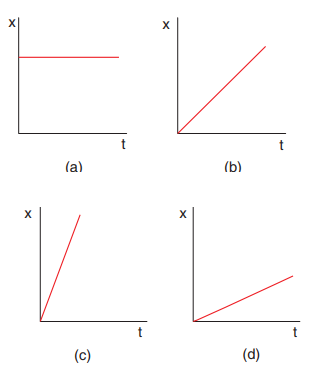
The slope in the position – time graph will give the speed of the particle.
In the graph (a) slope is zero. Graph has higher slope than graphs (b) and So we can arrange the speeds in ascending order as
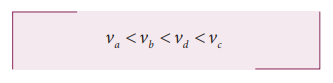
Solved Example Problem for Addition of Vectors
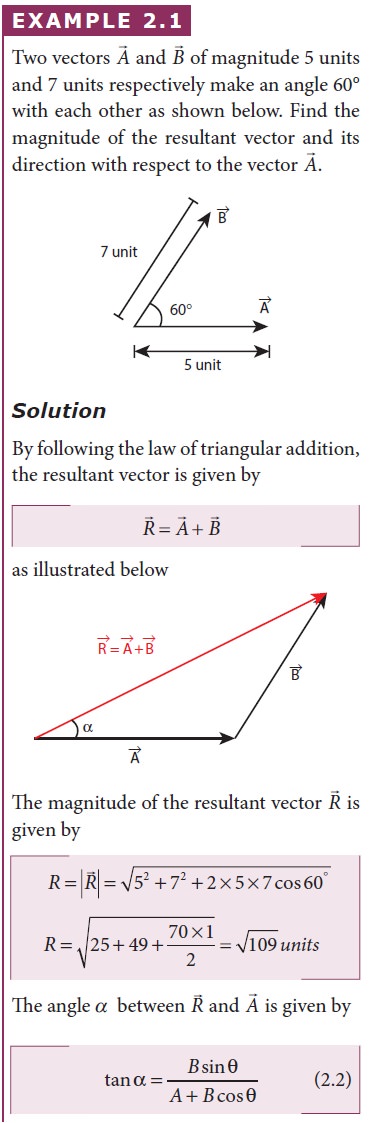

Solved Example Problem for Subtraction of vectors

EXAMPLE 2.3
What are the unit vectors along the negative x–direction, negative y–direction, and negative z– direction?
Solution
The unit vectors along the negative directions can be shown as in the following figure.
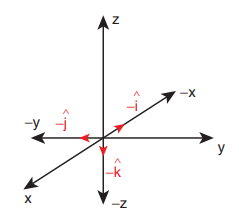
Then we have:
The unit vector along the negative x direction = -iˆ
The unit vector along the negative y direction = -jˆ.
The unit vector along the negative z direction = -kˆ.
Vector addition using components
In the previous section we have learnt about addition and subtraction of two vectors using geometric methods. But once we choose a coordinate system, the addition and subtraction of vectors becomes much easier to perform.
The two vectors ![]() and
and ![]() in a Cartesian coordinate system can be expressed as
in a Cartesian coordinate system can be expressed as

Then the addition of two vectors is equivalent to adding their corresponding x, y and z components.

Similarly the subtraction of two vectors is equivalent to subtracting the corresponding x, y and z components.
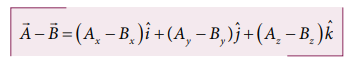
The above rules form an analytical way of adding and subtracting two vectors.

Solved Example Problems for Multiplication Of Vector By A Scalar

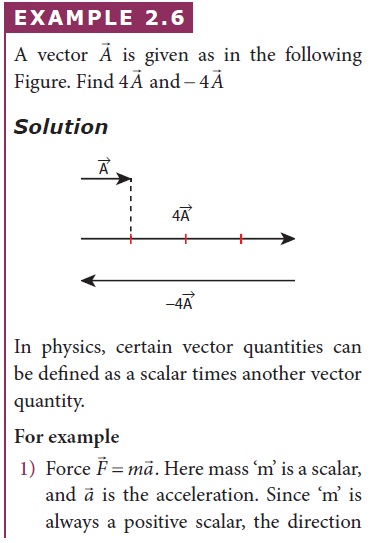

Solved Example Problems for Scalar Product of Two Vectors


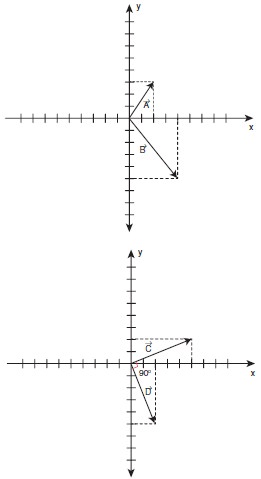
Solved Example Problems for The Vector Product of Two Vectors

Solved Example Problems for Properties of the components of vectors



Solved Example Problems for Position Vector
EXAMPLE 2.13
Determine the position vectors for the following particles which are located at points P, Q, R, S.

Example 2.14
A person initially at rest starts to walk 2 m towards north, then 1 m towards east, then 5 m towards south and then 3 m towards west. What is the position vector of the person at the end of the trip?
Solution
As shown in the Figure, the positive x axis is taken as east direction, positive y direction is taken as north.
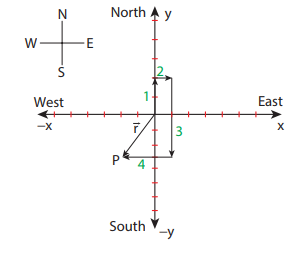
After the trip, the person reaches the point P whose position vector given by
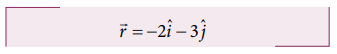
The displacement direction is south west.
Solved Example Problems for Distance and Displacement
Example 2.15
Assume your school is located 2 km away from your home. In the morning you are going to school and in the evening you come back home. In this entire trip what is the distance travelled and the displacement covered?
Solution
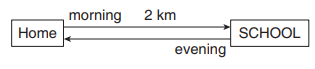
The displacement covered is zero. It is because your initial and final positions are the same.
But the distance travelled is 4 km.
Example 2.16
An athlete covers 3 rounds on a circular track of radius 50 m. Calculate the total distance and displacement travelled by him.
Solution

The total distance the athlete covered =3x circumference of track
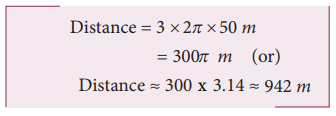
The displacement is zero, since the athlete reaches the same point A after three rounds from where he started.
Solved Example Problems for Displacement Vector in Cartesian Coordinate System
Example 2.17
Calculate the displacement vector for a particle moving from a point P to Q as shown below. Calculate the magnitude of displacement.

Solution

Solved Example Problems for Differential Calculus
Example 2.18
Consider the function y = x 2 . Calculate the derivative dy/dx using the concept of limit.
Solution
Let us take two points given by


These results are tabulated as shown below:
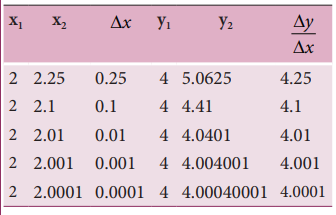
From the above table, the following inferences can be made.

Example 2.19
Find the derivative with respect to t, of the function x= A0 + A1t + A2 t2 where A0, A1 and A2 are constants.
Solution
Note that here the independent variable is ‘t’ and the dependent variable is ‘x’
The requived derivative is dx/dt = 0+ A1+2A2t
The second derivative is d2x/d2t = 2A2
Solved Example Problems for Average speed
Example 2.20
Consider an object travelling in a semi-circular path from point O to point P in 5 second, as is shown in the Figure. Calculate the average velocity and average speed.
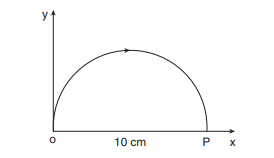
Solution
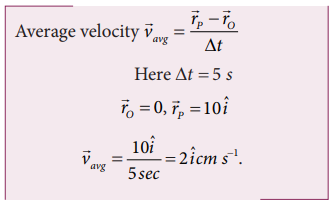
The average velocity is in the positive x direction.
The average speed = total path length / time taken (the path is semi-circular)

Note that the average speed is greater than the magnitude of the average velocity.
Solved Example Problems Instantaneous velocity or velocity
Example 2.21
The position vector of a particle is given 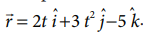
Calculate the velocity and speed of the particle at any instant t
Calculate the velocity and speed of the particle at time t = 2 s
Solution

Note that the particle has velocity components along x and y direction. Along the z direction the position has constant value (-5) which is independent of time. Hence there is no z-component for the velocity.
Example 2.22
The velocity of three particles A, B, C are given below. Which particle travels at the greatest speed?
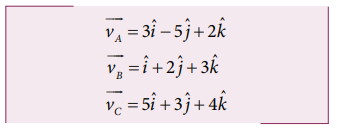
Solution
We know that speed is the magnitude of the velocity vector. Hence,

The particle C has the greatest speed.
Example 2.23
Two cars are travelling with respective velocities ![]() =10ms-1 along east and
=10ms-1 along east and ![]() =10ms-1 along west What are the speeds of the cars?
=10ms-1 along west What are the speeds of the cars?
Solution
Both cars have the same magnitude of velocity. This implies that both cars travel at the same speed even though they have velocities in different directions. Speed will not give the direction of motion.

Solved Example Problems Momentum
Example 2.24
Consider two masses of 10 g and 1 kg moving with the same speed 10 m s-1. Calculate the magnitude of the momentum.
Solution
We use p = mv
For the mass of 10 g, m = 0.01 kg

Thus even though both the masses have the same speed, the momentum of the heavier mass is 100 times greater than that of the lighter mass.
Solved Example Problems for Average velocity
Example 2.25
A particle moves along the x-axis in such a way that its coordinates x varies with time 't' according to the equation x = 2 - 5t + 6t2. What is the initial velocity of the particle?
Solution

The negative sign implies that at t = 0 the velocity of the particle is along negative x direction.
Solved Example Problems for Relative Velocity in One and Two Dimensional Motion
Example 2.26
Suppose two cars A and B are moving with uniform velocities with respect to ground along parallel tracks and in the same direction. Let the velocities of A and B be 35 km h-1 due east and 40 km h-1 due east respectively. What is the relative velocity of car B with respect to A?
Solution
The relative velocity of B with respect to A, 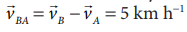 due east
due east
Similarly, the relative velocity of A with respect to B i.e., 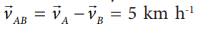 due west.
due west.
Example 2.27
Suppose two trains A and B are moving with uniform velocities along parallel tracks but in opposite directions. Let the velocity of train A be 40 km h-1 due east and that of train B be 40 km h-1 due west. Calculate the relative velocities of the trains
Solution
Relative velocity of A with respect to B, vAB = 80 km h−1 due east
Thus to a passenger in train B, the train A will appear to move east with a velocity of 80 km h−1
The relative velocity of B with respect to A, VBA = 80 km h−1 due west
To a passenger in train A, the train B will appear to move westwards with a velocity of 80 km h−1
Example 2.28
Consider two trains A and B moving along parallel tracks with the same velocity in the same direction. Let the velocity of each train be 50 km h-1 due east. Calculate the relative velocities of the trains
Solution

Similarly, relative velocity of A with respect to B i.e., vAB is also zero.
Thus each train will appear to be at rest with respect to the other.
Example 2.29
How long will a boy sitting near the window of a train travelling at 36 km h-1 see a train passing by in the opposite direction with a speed of 18 km h-1. The length of the slow-moving train is 90 m.
Solution
The relative velocity of the slow-moving train with respect to the boy is = (36 + 18) km h-1 = 54 km h-1 = = 54 × 5/18 ms-1 = 15 m s-1
Since the boy will watch the full length of the other train, to find the time taken to watch the full train:
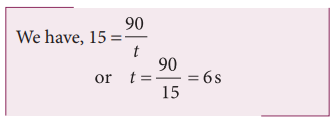
Example 2.30
A swimmer’s speed in the direction of flow of a river is 12 km h-1. Against the direction of flow of the river the swimmer’s speed is 6 km h-1. Calculate the swimmer’s speed in still water and the velocity of the river flow.
Solution
Let vs and vr , represent the velocities of the swimmer and river respectively with respect to ground.

When the river flow and swimmer move in the same direction, the net velocity of swimmer is 12 km p h-1.
Solved Example Problems for Accelerated Motion
Example 2.31
A velocity–time graph is given for a particle moving in x direction, as below
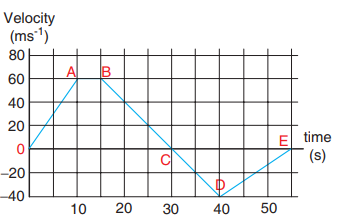
a) Describe the motion qualitatively in the interval 0 to 55 s .
b) Find the distance and displacement travelled from 0 s to 40 s .
c) Find the acceleration at t = 5 s and at t = 20 s
Solution
a) From O to A: (0 s to 10 s )
At t = 0 s the particle has zero velocity.
At t > 0, particle has positive velocity and moves in the positive x direction.
From 0 s to 10 s the slope (dv/dt) positive, implying the particle is accelerating. Thus the velocity increases during this time interval.
From A to B: (10 s to 15 s )
From 10 s to 15 s the velocity stays constant at 60 m s-1. The acceleration is 0 during this period. But the particle continues to travel in the positive x-direction.
From B to C : (15 s to 30 s )
From the 15 s to 30 s the slope is negative, implying the velocity is decreasing. But the particle is moving in the positive x direction. At t = 30 s the velocity becomes zero, and the particle comes to rest momentarily at t = 30 s .
From C to D: (30 s to 40 s )
From 30 s to 40 s the velocity is negative. It implies that the particle starts to move in the negative x direction. The magnitude of velocity increases to a maximum 40 m s-1
From D to E: (40 s to 55 s )
From 40 s to 55 s the velocity is still negative, but starts increasing from –40 m s-1 At t = 55 s the velocity of the particle is zero and particle comes to rest.
(b) The total area under the curve from 0 s to 40 s will give the displacement. Here the area from O to C represents motion along positive x–direction and the area under the graph from C to D represents the particle's motion along negative x–direction.
The displacement travelled by the particle from 0 s to 10 s = 1/2 × 10 × 60 = 300m
The displacement travelled from 10 s to 15 s = 60 × 5 = 300 m
The displacement travelled from 15 s to 30 s =1/2 × 15 × 60 = 450m
The displacement travelled from 30 s to 40 s = 1/2 × 10 × (-40) = -200m.
Here the negative sign implies that the particle travels 200 m in the negative x direction.

300 m + 300 m + 450 m − 200 m = +850 m.
Thus the particle's net displacement is along the positive x-direction.
The total distance travelled by the
particle from 0 s to 40 s = 300 + 300 + 450 + 200 = 1250 m.
(c) The acceleration is given by the slope in the velocity-time graph. In the first 10 seconds the velocity has constant slope (constant acceleration). It implies that the acceleration a is from v1 = 0 to v2 = 60 m s-1.
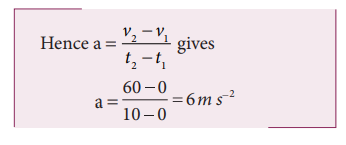
Next, the particle has constant negative slope from 15 s to 30 s . In this case v2=0 and v1=60m s-1. Thus the acceleration at t = 20 s is given by a = (0-60)/(30-15) = 4 m s-2. Here the negative sign implies that the particle has negative acceleration.
Example 2.32
If the position vector of the particle is given by 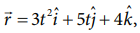 Find the
Find the
a. The velocity of the particle at t = 3 s
b. Speed of the particle at t = 3 s
c. acceleration of the particle at time t = 3 s
Solution

Example 2.33
An object is thrown vertically downward. What is the acceleration experienced by the object?
Solution
We know that when the object falls towards the Earth, it experiences acceleration due to gravity g = 9.8 m s-2 downward. We can choose the coordinate system as shown in the figure.
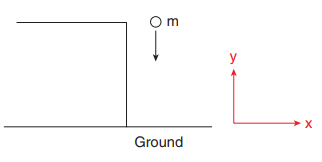
The acceleration is along the negative y direction.
Solved Example Problems for motion under gravity: Case (1): A body falling from a height h
Example 2.34
An iron ball and a feather are both falling from a height of 10 m.
a) What are the time taken by the iron ball and feather to reach the ground?
b) What are the velocities of iron ball and feather when they reach the ground?
(Ignore air resistance and take g = 10 m s-2)
Solution
Since kinematic equations are independent of mass of the object, according to equation (2.8) the time taken by both iron ball and feather to reach the ground are the same. This is given by

Thus, both feather and iron ball reach ground at the same time.
By following equation (2.19) both iron ball and feather reach the Earth with the same speed. It is given by

Example 2.35
Is it possible to measure the depth of a well using kinematic equations?

Consider a well without water, of some depth d. Take a small object (for example lemon) and a stopwatch. When you drop the lemon, start the stop watch. As soon as the lemon touches the bottom of the well, stop the watch. Note the time taken by the lemon to reach the bottom and denote the time as t.
Since the initial velocity of lemon u = 0 and the acceleration due to gravity g is constant over the well, we can use the equations of motion for constant acceleration.

Since u = 0, s = d, a = g (Since we choose the y axis downwards), Then
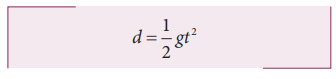
Substituting g = 9.8 m s-2 we get the depth of the well.

To estimate the error in our calculation we can use another method to measure the depth of the well. Take a long rope and hang the rope inside the well till it touches the bottom. Measure the length of the rope which is the correct depth of the well (dcorrect ). Then

What would be the reason for an error, if any?
Repeat the experiment for different masses and compare the result with dcorrect every time.
Solved Example Problems for motion under gravity: Case (2): A body thrown vertically upwards
Example 2.36
A train was moving at the rate of 54 km h-1 when brakes were applied. It came to rest within a distance of 225 m. Calculate the retardation produced in the train.
Solution
The final velocity of the particle v = 0
The initial velocity of the particle
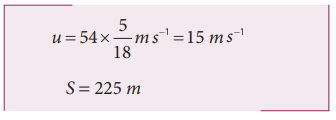
Retardation is always against the velocity of the particle.

Solved Example Problems for Projectile Motion
Example 2.37
Suppose an object is thrown with initial speed 10 m s-1 at an angle π/4 with the horizontal, what is the range covered? Suppose the same object is thrown similarly in the Moon, will there be any change in the range? If yes, what is the change? (The acceleration due to gravity in the Moon gmoon = 1/6 g)
Solution
In projectile motion, the range of particle is given by,

If the same object is thrown in the Moon, the range will increase because in the Moon, the acceleration due to gravity is smaller than g on Earth,

The range attained on the Moon is approximately six times that on Earth.
Example 2.38
In the cricket game, a batsman strikes the ball such that it moves with the speed 30 m s-1 at an angle 30o with the horizontal as shown in the figure. The boundary line of the cricket ground is located at a distance of 75 m from the batsman? Will the ball go for a six? (Neglect the air resistance and take acceleration due to gravity g = 10 m s-2).
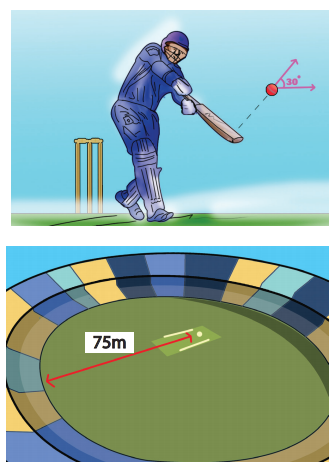
Solution
The motion of the cricket ball in air is essentially a projectile motion. As we have already seen, the range (horizontal distance) of the projectile motion is given by
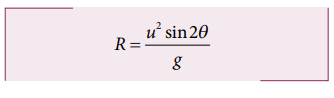
The initial speed u ![]() 30 m s-1
30 m s-1
The projection angle θ = 30o
The horizontal distance travelled by the cricket ball
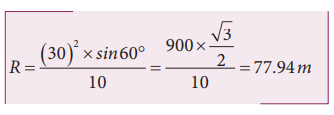
This distance is greater than the distance of the boundary line. Hence the ball will cross this line and go for a six.
Solved Example Problems for Degrees and Radians
Example 2.39
Calculate the angle θ subtended by the two adjacent wooden spokes of a bullock cart wheel is shown in the figure. Express the angle in both radian and degree.

Solution
The full wheel subtends 2π radians at the center of the wheel. The wheel is divided into 12 parts (arcs).

The angle subtended by two adjacent wooden spokes is 30 degree at the center.
Solved Example Problems for Circular Motion
Example 2.40
A particle moves in a circle of radius 10 m. Its linear speed is given by v = 3t where t is in second and v is in m s-1.
a) Find the centripetal and tangential acceleration at t = 2 s.
b) Calculate the angle between the resultant acceleration and the radius vector.
Solution
The linear speed at t = 2 s
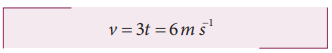
The centripetal acceleration at t = 2 s is
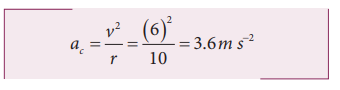
The angle between the radius vector with resultant acceleration is given by
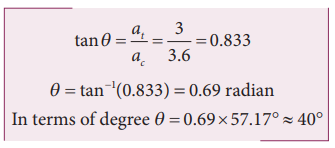
Example 2.41
A particle is in circular motion with an acceleration α = 0.2 rad s−2.
a) What is the angular displacement made by the particle after 5 s?
b) What is the angular velocity at t = 5 s?. Assume the initial angular velocity is zero.
Solution
Since the initial angular velocity is zero (ω0 = 0).
The angular displacement made by the particle is given by
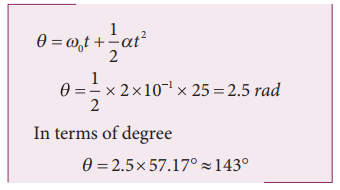
Related Topics