Angular displacement in Projectile Motion

Angular displacement

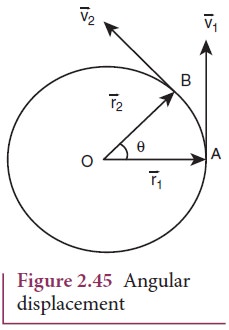
Consider a particle revolving around a point O in a circle of radius r (Figure 2.45). Let the position of the particle at time t = 0 be A and after time t, its position is B.

Then,

The angle described by the particle about the axis of rotation (or center O) in a given time is called angular displacement.

i.e., angular displacement = ∠AOB =θ

The unit of angular displacement is radian.

The angular displacement (θ) in radian is related to arc length S (AB) and radius r as

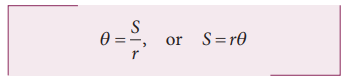
Angular velocity(Vector ω−>)

The rate of change of angular displacement is called angular velocity.

If θ is the angular displacement in time t, then the angular velocity ω is

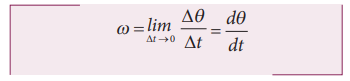
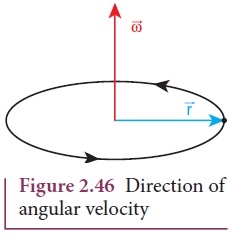
The unit of angular velocity is radian per second (rad s⁻¹). The direction of angular velocity is along the axis of rotation following the right hand rule. This is shown in Figure 2.46.

Angular acceleration (α)

The rate of change of angular velocity is called angular acceleration.

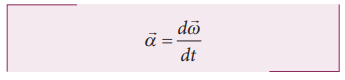
The angular acceleration is also a vector quantity which need not be in the same direction as angular velocity.

Tangential acceleration

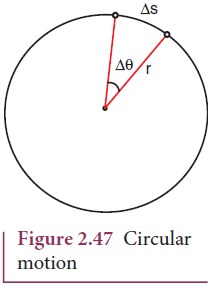
Consider an object moving along a circle of radius r. In a time ∆t, the object travels an arc distance ∆s as shown in Figure 2.47. The corresponding angle subtended is Δθ

which gives the relation between linear speed and angular speed.

Equation (2.38) is true only for circular motion. In general the relation between linear and angular velocity is given by

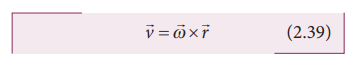
For circular motion equation (2.39) reduces to equation (2.38) since  and  are perpendicular to each other.

Differentiating the equation (2.38) with respect to time, we get (since r is constant)

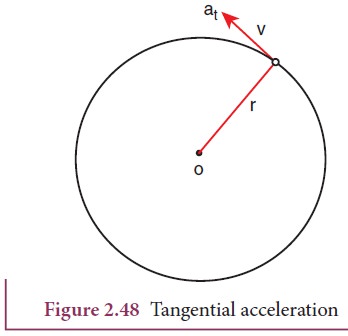
The tangential acceleration a_t experienced by an object is circular motion as shown in Figure 2.48.

Note that the tangential acceleration is in the direction of linear velocity.