Chapter: 11th Physics : UNIT 2 : Kinematics
Relative Velocity in One and Two Dimensional Motion
Relative Velocity in One and Two Dimensional Motion
When two objects A and B are moving with different velocities, then the velocity of one object A with respect to another object B is called relative velocity of object A with respect to B.
Case 1
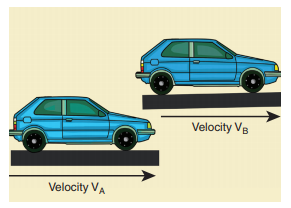
Consider two objects A and B moving with uniform velocities VA and VB, as shown, along straight tracks in the same direction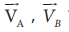 
with respect to ground.
The relative velocity of object A with respect to object B is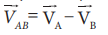 
The relative velocity of object B with respect to object A is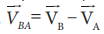 
Thus, if two objects are moving in the same direction, the magnitude of relative velocity of one object with respect to another is equal to the difference in magnitude of two velocities.
Case 2
Consider two objects A and B moving with uniform velocities VA and VB along the same straight tracks but opposite in direction
Thus, if two objects are moving in opposite directions, the magnitude of relative velocity of one object with respect to other is equal to the sum of magnitude of their velocities.
Case 3
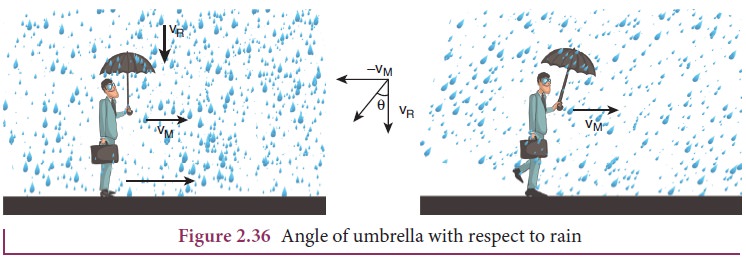
In order to save himself from the rain, he should hold an umbrella at an angle θ with the vertical.
Accelerated Motion
During non-uniform motion of an object, the velocity of the object changes from instant to instant i.e., the velocity of the object is no more constant but changes with time. Such a motion is said to be an accelerated motion.
· In accelerated motion, if the change in velocity of an object per unit time is same (constant) then the object is said to be moving with uniformly accelerated motion.
· On the other hand, if the change in velocity per unit time is different at different times, then the object is said to be moving with non-uniform accelerated motion.
Average acceleration
If an object changes its velocity from 
to 
in a time interval ∆t = t 2 − t 1 , then the average acceleration is defined as the ratio of change in velocity over the time interval ∆t = t 2 − t1
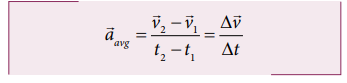
Average acceleration is a vector quantity in the same direction as the vector ∆
.
Instantaneous acceleration
Usually, the average acceleration will give the change in velocity only over the entire time interval. It will not give value of the acceleration at any instant time t.
Instantaneous acceleration or acceleration of a particle at time ‘t’ is given by the ratio of change in velocity over Δt, as Δt approaches zero.
In other words, the acceleration of the particle at an instant t is equal to rate of change of velocity.
i. Acceleration is a vector quantity. Its SI unit is ms-2 and its dimensional formula is M0L1T-2
ii. Acceleration is positive if its velocity is increasing, and is negative if the velocity is decreasing. The negative acceleration is called retardation or deceleration.
In terms of components, we can write
Since each component of velocity is the derivative of the corresponding coordinate, we can express the components ax, ay, and az, as
Thus acceleration is the second derivative of position vector with respect to time.
Graphically the acceleration is the slope in the velocity-time graph. At the same time if the acceleration-time graph is given, then the velocity can be found from the area under the acceleration-time graph.
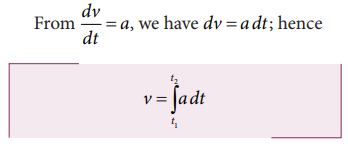
For an initial time t1 and final time t2
Solved Example Problems for Relative Velocity in One and Two Dimensional Motion
Example 2.26
Suppose two cars A and B are moving with uniform velocities with respect to ground along parallel tracks and in the same direction. Let the velocities of A and B be 35 km h-1 due east and 40 km h-1 due east respectively. What is the relative velocity of car B with respect to A?
Solution
The relative velocity of B with respect to A,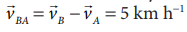 
due east
Similarly, the relative velocity of A with respect to B i.e.,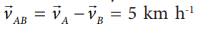 
due west.
Example 2.27
Suppose two trains A and B are moving with uniform velocities along parallel tracks but in opposite directions. Let the velocity of train A be 40 km h-1 due east and that of train B be 40 km h-1 due west. Calculate the relative velocities of the trains
Solution
Relative velocity of A with respect to B, vAB = 80 km h−1 due east
Thus to a passenger in train B, the train A will appear to move east with a velocity of 80 km h−1
The relative velocity of B with respect to A, VBA = 80 km h−1 due west
To a passenger in train A, the train B will appear to move westwards with a velocity of 80 km h−1
Example 2.28
Consider two trains A and B moving along parallel tracks with the same velocity in the same direction. Let the velocity of each train be 50 km h-1 due east. Calculate the relative velocities of the trains
Solution
Similarly, relative velocity of A with respect to B i.e., vAB is also zero.
Thus each train will appear to be at rest with respect to the other.
Example 2.29
How long will a boy sitting near the window of a train travelling at 36 km h-1 see a train passing by in the opposite direction with a speed of 18 km h-1. The length of the slow-moving train is 90 m.
Solution
The relative velocity of the slow-moving train with respect to the boy is = (36 + 18) km h-1 = 54 km h-1 = = 54 × 5/18 ms-1 = 15 m s-1
Since the boy will watch the full length of the other train, to find the time taken to watch the full train:
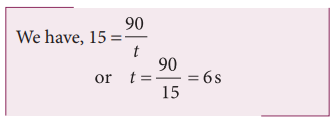
Example 2.30
A swimmer’s speed in the direction of flow of a river is 12 km h-1. Against the direction of flow of the river the swimmer’s speed is 6 km h-1. Calculate the swimmer’s speed in still water and the velocity of the river flow.
Solution
Let vs and vr , represent the velocities of the swimmer and river respectively with respect to ground.
When the river flow and swimmer move in the same direction, the net velocity of swimmer is 12 km p h-1.
Related Topics