Physics - Kinematics: Important Questions | 11th Physics : UNIT 2 : Kinematics
Chapter: 11th Physics : UNIT 2 : Kinematics
Kinematics: Important Questions
Short Answer
Questions
1.
Explain what is meant by Cartesian coordinate system?
2.
Define a vector. Give examples
3.
Define a scalar. Give examples
4.
Write a short note on the scalar product between two vectors.
5.
Write a short note on vector product between two vectors.
6.
How do you deduce that two vectors are perpendicular?
7.
Define displacement and distance.
8.
Define velocity and speed.
9.
Define acceleration.
10.
What is the difference between velocity and average velocity.
11.
Define a radian?
12.
Define angular displacement and angular velocity.
13.
What is non uniform circular motion?
14.
Write down the kinematic equations for angular motion.
15.
Write down the expression for angle made by resultant acceleration and radius
vector in the non uniform circular motion.
Long Answer
Questions
1.
Explain in detail the triangle law of addition.
2.
Discuss the properties of scalar and vector products.
3.
Derive the kinematic equations of motion for constant acceleration.
4.
Derive the equations of motion for a particle (a) falling vertically (b)
projected vertically
5.
Derive the equation of motion, range and maximum height reached by the particle
thrown at an oblique angle θ with respect to the horizontal direction.
6.
Derive the expression for centripetal acceleration.
7.
Derive the expression for total acceleration in the non uniform circular
motion.
Exercises
1. The position vectors particle has length 1m and makes 30° with the x-axis. What are the lengths of the x and y components of the position vector?




6. An object at an angle such that the horizontal range is 4 times of the maximum height. What is the angle of projection of the object?
[Ans: θ = 45°]

7. The following graphs represent velocity – time graph. Identify what kind of motion a particle undergoes in each graph.

Answers:
(a) (i) It represents the uniform acceleration.
Body starts from nest and move with constant velocity
(ii) Greater is the slope v – (1/N)t graph, greater will be the acceleration.
(b) Body moving with uniform velocity, zero slope indicates zero acceleration.
(c) Straight line v (1/N)t graph does not pass the origin. After some time it moves with a uniform acceleration, [acceleration is constant but greater than first graph]
(d) Greater changes in velocity are taking place in equal intervals of time. It represents an increasing acceleration ie. acceleration is variable.
8. The following velocity–time graph represents a particle moving in the positive x–direction. Analyse its motion from 0 to 7 s. Calculate the displacement covered and distance travelled by the particle from 0 to 2 s.
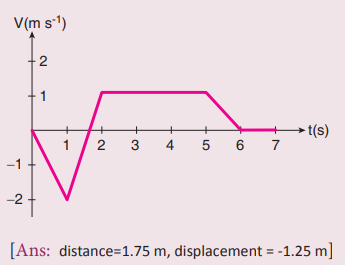
Answers:
It is uniform motion
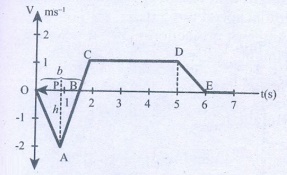
Distance travelled by the particle
= area of ΔOAB = 1/2 × b × h
OB = b; PA = h
= ½ × 1.5 × 2 = 1.5m
Displacement covered = + ½ × b × h
= ½ × 1.5 × (-2)
A particle moves with -ve velocity along OA, then moves with uniform Velocity and retards uniformly then it comes to rest at E.
9. A particle is projected at an angle of T with respect to the horizontal direction. Match the following for the above motion.
Ans: Position vector – remains downward
Answers:
(a) vx - remains constant
(b) vy - decreases and increases
(c) Acceleration - remains downward
(d) Position vector - varies
[Ans: v x : remains constant ͕ v y : decreases and increases, a remains downward, r: varies]
10. A water fountain on the ground sprinkles water all around it. If the speed of the water coming out of the fountain is v. Calculate the total area around the fountain that gets wet.
Answers:
Speed of the water coming out of the fountion - v
The maximum distance the water wets = Rmax
Total area around the fountain that gets wet = A = ?
A = πR2max.
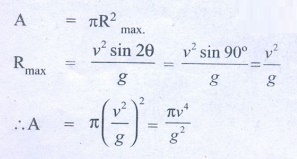
[Ans: Area = πv2/g2]
11. The following table gives the range of a particle when thrown on different planets. All the particles are thrown at the same angle with the horizontal and with the same initial speed. Arrange the planets in ascending order according to their acceleration due to gravity, (g value).
Planet Range
Jupiter 50 m
Earth 75 m
Mars 90 m
Mercury 95 m
Answers:
(Ascending order)
1. Jupiter 50 m – greater ‘g’ value.
2. Earth 75 m
3. Mars 90 m
4. Mercury – Smaller ‘g’ value.
[Ans: g jupiter is greater, gmercury is smaller]
12. The resultant of two vectors A and B is perpendicular to vector A and its magnitude is equal to half of the magnitude of vector B. Then the angle between A and B is
a) 30° b) 45° c) 150° d) 120°
Answers:
Resultant of two vectors A & B = R
Magnitude of R = B/2
Angle between A & B = ?
R = B sin θ => B/2 = B sin θ
Sin θ = (B/2) / B = ½
θ = 30°
The angle between A & B = 180° - 30° = 150°.
[Ans: θ = 150°]
13. Compare the components for the following vector equations
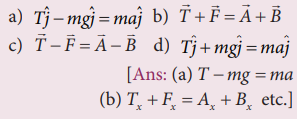
Answer:
(a) T - mg = ma
(b) Tx + Fx = Ax + Bxetc.
(c) Tx -Fx = Ax - Bx etc.
(d) T + mg = ma
14. Calculate the area of the triangle for which two of its sides are given by the vectors
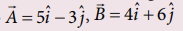
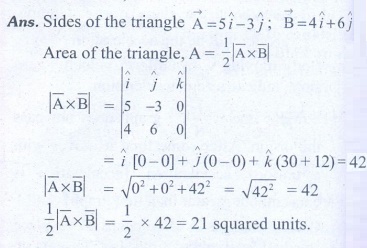
[Ans: Area = 21]
15. If Earth completes one revolution in 24hours, what is the angular displacement made by Earth in one hour. Express your answer in both radian and degree.
Answers:
Time taken for earth to complete one revolution = 24 hr
Angle covered by θ = 360° = 2π radians
For one revolution i.e. 24 hrs, the angular displacement is 2π radians
For one hour, the angular displacement
θ = 2π/24 = π/12
(or)
180°/12 = 15°
θ = π /12 or 15°.
[Ans: θ = 15°or π/12 ]
16. A object is thrown with initial speed 5 ms−1 with an angle of projection 30γ. What is the height and range reached by the particle?

[Ans: height = 0.318 m Range =2.21 m]
17. A foot-ball player hits the ball with speed 20 m s-1 with angle 30° with respect to horizontal direction as shown in the figure. The goal post is at distance of 40 m from him. Find out whether ball reaches the goal post?

Answers:
The speed of the ball, u = 20 m/s.
Angle of projection θ = 30°; g = 9.8 ms-2
Horizontal distance R = ?
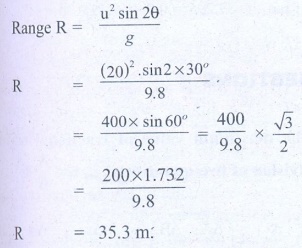
R = 35.3 m.'
The goal post is. at a distance of 40 m , But horizontal distance is 35.3 m. So the ball will not reach the goal post.
[Ans: Ball will not reach the goal post. The range =35.3 m]
18 .If an object is thrown horizontally with an initial speed 10 m s−1 from the top of a building of height 100 m. what is the horizontal distance covered by the particle?
Answer:
h = - 100 m
g = -9.8 m/s2
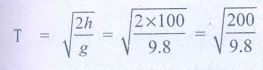
= √(20.408) = 4.51 seconds.
Horizontal distance R = u × T
= 10 × 4.51 =45.1 m.
[Ans: R= 45 m]
19. An object is executing uniform circular motion with an angular speed of π/12 radian per second. At t = 0 the object starts at an angle θ = 0 What is the angular displacement of the particle after 4 s ?

[Ans: 30°]
20. Consider the x–axis as representing east, the y–axis as north and z–axis as vertically upwards. Give the vector representing each of the following points.
Ans: 5 m north east and 2 m up


21. The Moon is orbiting the Earth approximately once in 27 days, what is the angle transversed by the Moon per day?
Answer:
Duration taken by the moon in orbiting the earth = 27 days (approx)
The angle transversed by moon per day = 360/27 = 13°3’
[Ans: 13°3’]
22. An object of mass m has angular acceleration α = 0.2rad s−2. What is the angular displacement covered by the object after 3 second? (Assume that the object started with angle zero with zero angular velocity).
Answer:
Angular acceleration α = 0.2 rad s-2
The angular displacement covered by the object after 3 seconds is,
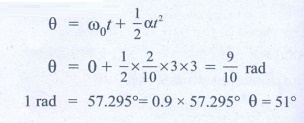
1 rad = 57.295°= 0.9 × 57.295°
θ = 51°
[Ans: 0.9 rad or 51°]
Related Topics