Solved Example Problem for Equations of motion under gravity

Solved Example Problems for motion under gravity: Case (1): A body falling from a height h

Example 2.34

An iron ball and a feather are both falling from a height of 10 m.

a) What are the time taken by the iron ball and feather to reach the ground?

b) What are the velocities of iron ball and feather when they reach the ground?

(Ignore air resistance and take g = 10 m s-2)

Solution

Since kinematic equations are independent of mass of the object, according to equation (2.8) the time taken by both iron ball and feather to reach the ground are the same. This is given by

Thus, both feather and iron ball reach ground at the same time.

By following equation (2.19) both iron ball and feather reach the Earth with the same speed. It is given by

Example 2.35

Is it possible to measure the depth of a well using kinematic equations?

Consider a well without water, of some depth d. Take a small object (for example lemon) and a stopwatch. When you drop the lemon, start the stop watch. As soon as the lemon touches the bottom of the well, stop the watch. Note the time taken by the lemon to reach the bottom and denote the time as t.

Since the initial velocity of lemon u = 0 and the acceleration due to gravity g is constant over the well, we can use the equations of motion for constant acceleration.

Since u = 0, s = d, a = g (Since we choose the y axis downwards), Then

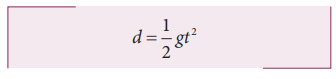
Substituting g = 9.8 m s-2 we get the depth of the well.

To estimate the error in our calculation we can use another method to measure the depth of the well. Take a long rope and hang the rope inside the well till it touches the bottom. Measure the length of the rope which is the correct depth of the well (dcorrect ). Then

What would be the reason for an error, if any?

Repeat  the  experiment  for  different masses and compare the result with dcorrect every time.

Solved Example Problems for motion under gravity: Case (2): A body thrown vertically upwards

Example 2.36

A train was moving at the rate of 54 km h-1 when brakes were applied. It came to rest within a distance of 225 m. Calculate the retardation produced in the train.

Solution

The final velocity of the particle v = 0

The initial velocity of the particle

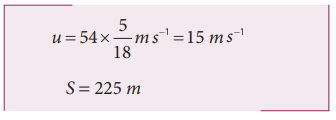
Retardation is always against the velocity of the particle.