Long Questions and Answer

Physics : Kinematics

Long Answer Questions

1. Explain in detail the triangle law of addition.

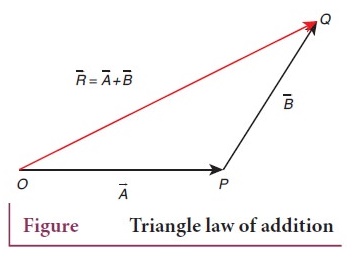
● The two vectors are represented by two adjacent sides of a triangle taken in the same order. Then the resultant is given by the third side of the triangle.

● The head of the first vector  is connected to the tail of second vector . 

● Let θ is the angle between  and . 

● R is the resultant vector connecting the tail of the first vector  to the head of the second vector .

●  

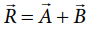
1) Magnitude of resultant Vector :

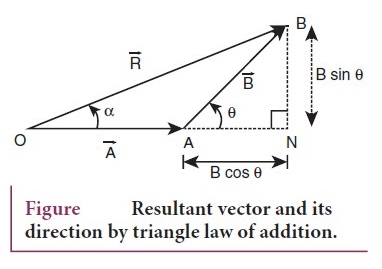
● Consider the triangle ABN which is obtained by extending the side OA to ON.

● ABN is a right angled triangle.

cos θ = AN / B       

∴ AN = B cos θ        ……… (1)

cos θ = BN / B

∴ AN = B cos θ        ……… (2)

For ∆ OBN, OB² = ON² + BN²        ……… (3)

R² = (A+B cosθ)² + (B sinθ)²

R² = A² + B² cos²θ + 2AB cos + B²sin²θ

R² = A² + B² (cos²θ sin²θ) + 2AB cosθ

R² = A² + B² + 2AB cosθ

R = √[A² + B² + 2AB cosθ]  ………… (4)

2. Direction of resultant Vectors :

If θ is the angle between  and  , then

In ∆OBN

tan α = BN / ON = BN / (OA + AN)

tan α = Bsinθ / (A + B cosθ)

∴ α = tan^-1 (Bsinθ / [A + B cosθ])       ……….(6)

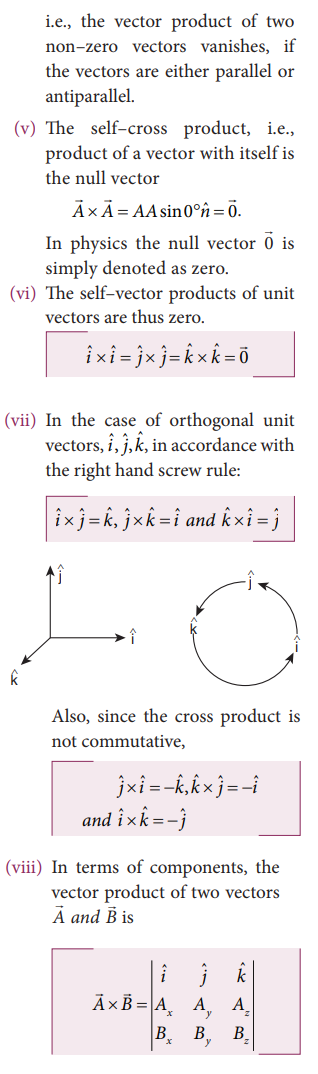
2. Discuss the properties of scalar and vector products.

Properties of scalar Product:

(i) The product quantity  .  is always a scalar. It is positive if the angle between the vectors is acute and negative if the angle between them is obtuse.

(ii) The scalar product is commutative

 .  =  . 

(iii) The vectors obey distributive law i,e,

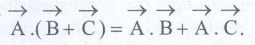
 (iv) The angle between the vectors

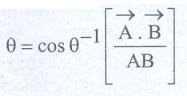
(v) The scalar product of two vectors will be maximum when cosθ = 1 i.e. θ = 0° When the vectors are parallel ( . )_max = AB

(vi) The scalar product of two vectors will be minimum when cosθ = −1 i.e. θ = 180° .

 ( . )_mini = −AB when the vectors are anti parallel.

vii) If the vectors  and  are perpendicular to each other then their scalar product  . = 0. Then the vectors  and  are said to be mutually orthogonal.

viii) The scalar product of a vector with itself is termed as self dot product and is given by

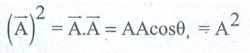
The magnitude (or) norm of the vectors  is || = A = √{.}

ix) In the case of a unit vector n^

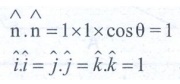
x) In the case of orthogonal unit vectors i^{^}, j^{^} and k^{^}

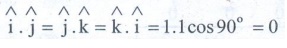
Properties of vector product:

3. Derive the kinematic equations of motion for constant acceleration.

● Consider an object moving in a straight line with uniform constant acceleration.

● Let u be the velocity of the object at time t = 0.

● v be the velocity of the body at a time t.

Velocity - time relation :

i) The acceleration of the body at any instant is given by the first derivative of velocity with respect to time.

a = dv / dt (or) dv = a.dt                 ……. (1)

Integrating on both sides

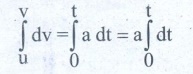
[v]_u^v = a [t]₀^t

v – u = at

v = u + at        ……..(2)

Displacement - time relation :

ii) The velocity of the body is given by the first derivative of the displacement with time.

v = ds / dt

ds = v.dt              …………….(3)

since v = u+at

ds = (u+at) dt          ……………. (4)

intergrating on both sides

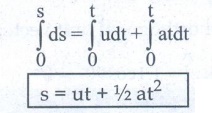
s = ut + ½ at²           …………(5)

Velocity - displacement relation:

iii) The acceleration is given by the first derivative of velocity with respect to time.

a = dv / dt = dv/ds . ds/dt = v . dv/ds           (ds / dt = v)

a = ½ dv²/ds

ds = 1/2a d(v²)         ………..(6)

Integrating on both sides

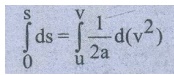
∴ s = 1/2a (v² – u²)

v² = u² + 2as      …………(7)

From equation

at = v - u        ……………. (8)

Substitute equation (8) in equation (5) we get,

s = ut+ ½ (v-u) t

s = [(u+v)t] / 2          …………(9)

Kinematic equations,

v = u+at

s = ut+ ½ at²

v² = u² + 2as

s = [(u+v)t ] / 2

4. Derive the equations of motion for a particle (a) falling vertically (b) projected vertically

i) A body falling vertically from a height h:

● Consider an object of mass in falling from a height h.

● Let us choose the downward direction as positive y axis.

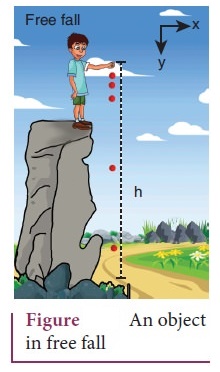
● The object experience acceleration 'g' due to granty which is constant near the surface of the earth. The acceleration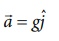 

By comparing the components we get, a_x =0, a_z =0, a_y = g

a_y = a = g

● If the particle is thrown with initial velocity u downward which is in negative y axis.

● Then velocity and position of the particle at any time t is given by,

v = u + gt  ……....... (1)

y = ut + ½ gt²       .......... (2)

The square of the speed of the particle is

v² = u² + 2gy     ......... (3)

Suppose the particle starts from rest

Then u = 0

v = gt        .......... (4)

y = ½ gt²         .......... (5)

 v² = 2gy      .......... (6)

b) A body thrown vertically upwards :

● An object of mass m thrown vertically up-wards with an initial velocity u.

● The acceleration a = −g and g points towards the negative y axis.

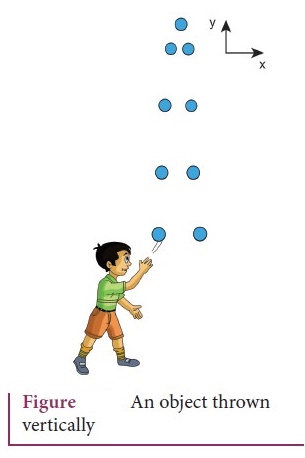
● The Kinematic equations for this motion are

v = u − gt  ………. (7)

s = ut – ½ gt²    ………. (8)

v² = u² -2gy

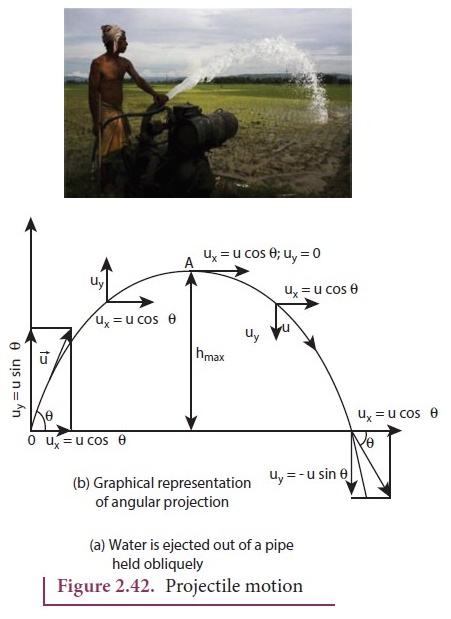
5. Derive the equation of motion, range and maximum height reached by the particle thrown at an oblique angle θ with respect to the horizontal direction.

● Consider an object thrown with initial velocity  u at an angle θ with the horizontal.

Then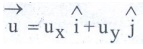 

Where u_x = u cos θ is the horizontal component.

u_y = u sinθ is the vertical component of velocity.

After the time t₁ the velocity along horizontal motion

v_x = u + a_x

t = u_x = u cosθ

The horizontal distance is

s_x = u_xt + ½a_xt²

Here s_x = x, u_x = u cosθ, a_x = 0

x = u cosθ.t

t = x / ucosθ        ………..(1)

For vertical motion v_y = u_y + a_yt

Here u_y = u sinθ, a_y = −g

v_y = u sinθ – gt      ………(2)

The vertical distance travelled by the projectile is

s_y = u_yt + ½ a_y t²

Here s_y = y, u_y = u sinθ, a_x = −g

than y = u sinθ.t – ½ gt²    ………(3)

Substitute the 't' value from the equation (1) in equation (3), we have

y = u sinθ [ x / ucosθ ]  –  ½ g [ x² / u² cos²θ ]   ………(4)

The path followed by the projectile is an inverted parabola.

Maximum (h_max )

The maximum vertical distance travelled by projectile during its journey is called maximum height.

For vertical part of motion,

v²_y = u²_y + 2a_yS

Here, u_y = u sinθ, a_y = −g, s = h_max ; v_y = 0

O = u²sin² θ − 2gh_max

h_max = u²sin²θ / 2g 

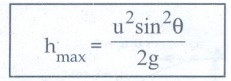      …………(5)

Horizontal Range (R):

The maximum horizontal distance between the point of projection and the point on the horizontal plane where the projectile hits the ground is called horizontal range (R).

Range R = Horizontal compoent of velocity × time of flight

R = u cosθ × T_f

R = ucosθ × [2u sinθ / g] = [ 2u² sinθ cosθ ] / g

R = [u² sin2θ] / g 

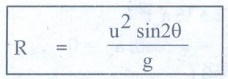           ……………… (6)

The maximum possible range is reached when sin2θ = l,

When 2θ = π /2 (or) θ = π /4

R_max = u² / g

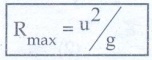       …………..(7)

6. Derive the expression for centripetal acceleration.

● The acceleration acting on an object towards the center of the circle in a uniform circular motion is known as centripetal acceleration.

● The centripetal acceleration is derived from a simple relationship between position and velocity vector.

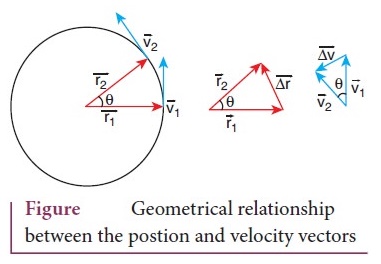
● The directions of position and velocity vectors shift through the same angle θ in small time ∆t as shown in the above figure

● For uniform circular motion r = |  | = |  | and  v = |  | = |  | 

● If the particle moves from position vector  to 

● The displacement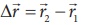  

● Then change in velocity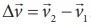 

then ∆r/r = - ∆v/v = θ        …………. (1)

Here negative sign implies that ∆v points radially inward, towards the centre of the circle.

∆v = −v (∆r / r)

a = ∆v / ∆t = v/r (∆r / ∆t) = −v² / r

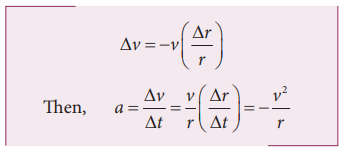
For uniform circular motion v = rω

Then centripetal acceleration a = −v² / r = - ω²r

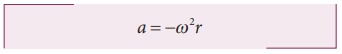
7. Derive the expression for total acceleration in the non uniform circular motion.

● If the speed of the object in circular motion is not constant then it is called non-uniform motion.

Example : The bob attached to a string moves in vertical circle.

● The speed of the bob is not the same at all time.

● The speed is not same in circular motion, the particle will have both centripetal and tangetial acceleration.

The centripetal acceleration is v²/r

The magnitude of resultant acceleration is

a_R = √ [ a_t² + (v² / r)² ]

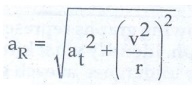
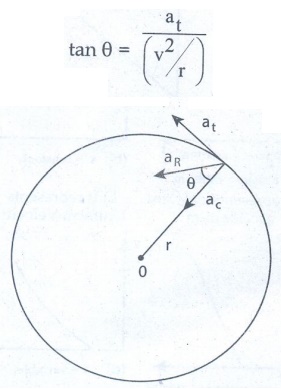
The resultant acceleration makes an angle θ with the radius vector.

The angle is given by tan θ = a_t / (v² / r)