Projectile under an angular projection

Projectile under an angular projection

This projectile motion takes place when the initial velocity is not horizontal, but at some angle with the vertical, as shown in Figure 2.42.

(Oblique projectile)

Examples :

·           Water ejected out of a hose pipe held obliquely.

·           Cannon fired in a battle ground.

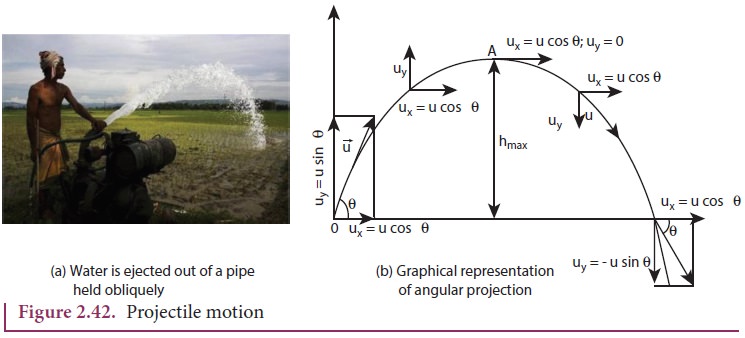
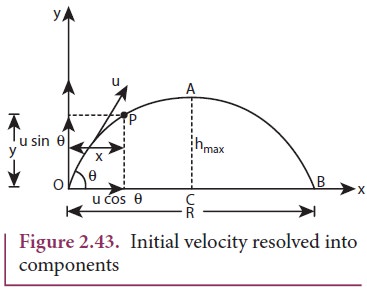
Consider an object thrown with initial velocity  at an angle θ  with the horizontal. Refer Figures 2.42 and 2.43.

Then

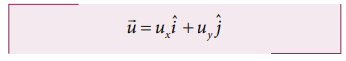
where ux = u cosθ is the horizontal component and uy = usinθ the vertical component of velocity.

Since the acceleration due to gravity is in the direction opposite to the direction of vertical component uy, this component will gradually reduce to zero at the maximum height of the projectile. At this maximum height, the same gravitational force will push the projectile to move downward and fall to the ground. There is no acceleration along the x direction throughout the motion. So, the horizontal component of the velocity (ux = u cosθ) remains the same till the object reaches the ground.

Hence after the time t, the velocity along horizontal motion vx = ux+ axt = ux = u cos θ

The horizontal distance travelled by projectile in time t is sx = uxt + 1/2 axt2

Here, sx = x, ux = u cosθ, ax = 0

Next, for the vertical motion vy = uy+ ayt

Here uy= u sinθ, ay = - g (acceleration due to gravity acts opposite to the motion). Thus

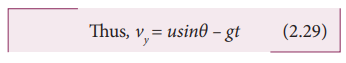
The vertical distance travelled by the projectile in the same time t is sy = uyt + 1/2 ayt2

Here, sy = y, uy = u sinθ, ax =-g. Then

Substitute the value of t from equation (2.28) in equation (2.30), we have

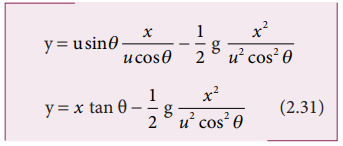
Thus the path followed by the projectile is an inverted parabola .

Maximum height (hmax)

The maximum vertical distance travelled by the projectile during its journey is called maximum height. This is determined as follows:

For the vertical part of the motion,

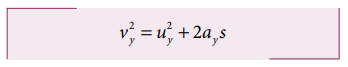
Here, uy = u sinθ, a =-g, s = hmax, and at the maximum height vy = 0

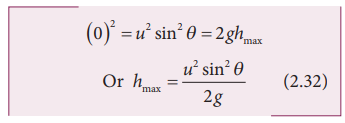
Time of flight (Tf)

The total time taken by the projectile from the point of projection till it hits the horizontal plane is called time of flight.

This time of flight is the time taken by the projectile to go from point O to B via point A (Figure 2.43)

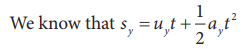
Here, sy = y = 0 (net displacement in y-direction is zero), uy = u sinθ, ay = -g, t = Tf  Then

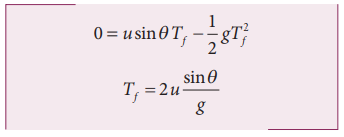
Horizontal range (R)

The maximum horizontal distance between the point of projection and the point on the horizontal plane where the projectile hits the ground is called horizontal range (R). This is found easily since the horizontal component of initial velocity remains the same. We can write

Range R = Horizontal component of velocity x time of flight = u cosθ ×Tf

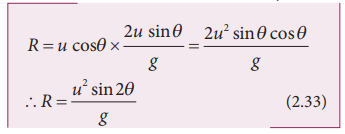
The horizontal range directly depends on the initial speed (u) and the sine of angle of projection (θ ). It inversely depends on acceleration due to gravity ‘g’

For a given initial speed u, the maximum possible range is reached when sin2θ is maximum, sin2θ = 1. This implies 2θ = π /2

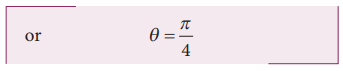
This means that if the particle is projected at 45 degrees with respect to horizontal, it attains maximum range, given by.

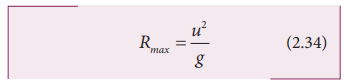
Solved Example Problems for Projectile Motion

Example 2.37

Suppose an object is thrown with initial speed 10 m s-1 at an angle π/4 with the horizontal, what is the range covered? Suppose the same object is thrown similarly in the Moon, will there be any change in the range? If yes, what is the change? (The acceleration due to gravity in the Moon gmoon = 1/6 g)

Solution

In projectile motion, the range of particle is given by,

If the same object is thrown in the Moon, the range will increase because in the Moon, the acceleration due to gravity is smaller than g on Earth,

The range attained on the Moon is approximately six times that on Earth.

Example 2.38

In the cricket game, a batsman strikes the ball such that it moves with the speed 30 m s-1  at an angle 30o with the horizontal as shown in the figure. The boundary line of the cricket ground is located at a distance of 75 m from the batsman? Will the ball go for a six? (Neglect the air resistance and take acceleration due to gravity g = 10 m s-2).

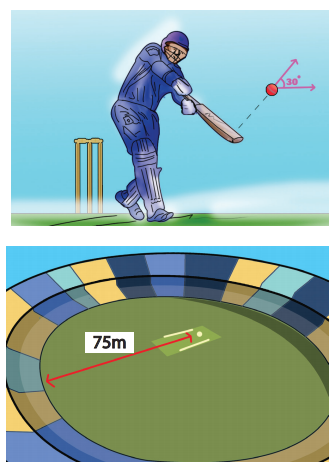
Solution

The motion of the cricket ball in air is essentially a projectile motion. As we have already seen, the range (horizontal distance) of the projectile motion is given by

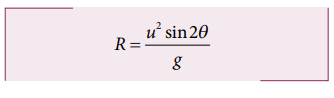
The initial speed u  30 m s-1

The projection angle θ = 30o

The horizontal distance travelled by the cricket ball

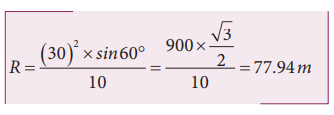
This distance is greater than the distance of the boundary line. Hence the ball will cross this line and go for a six.