Chapter: 11th Physics : UNIT 2 : Kinematics
Projectile in horizontal projection
Projectile in horizontal projection
Consider a projectile, say a ball, thrown horizontally with an initial velocity ![]() from the top of a tower of height h (Figure 2.39).
from the top of a tower of height h (Figure 2.39).
As the ball moves, it covers a horizontal distance due to its uniform horizontal
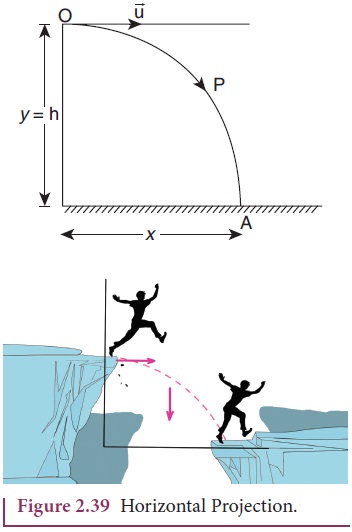
Thus, under the combined effect the ball moves along the path OPA. The motion is in a 2-dimensional plane. Let the ball take time t to reach the ground at point A, Then the horizontal distance travelled by the ball is x (t) = x, and the vertical distance travelled is y (t) = y
We can apply the kinematic equations along the x direction and y direction separately. Since this is two-dimensional motion, the velocity will have both horizontal component ux and vertical component uy.
Motion along horizontal direction
The particle has zero acceleration along x direction. So, the initial velocity ux remains constant throughout the motion
The distance traveled by the projectile at a time t is given by the equation x = uxt + 1/2 at2. Since a = 0 along x direction, we have

Motion along downward direction
Here uy = 0 (initial velocity has no downward component), a = g (we choose the +ve y-axis in downward direction), and distance y at time t
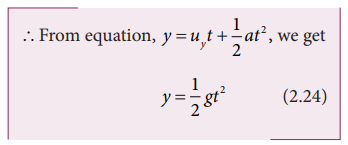
Substituting the value of t from equation (2.23) in equation (2.24) we have

Equation (2.25) is the equation of a parabola. Thus, the path followed by the projectile is a parabola (curve OPA in the Figure 2.39).
(1) Time of Flight: The time taken for the projectile to complete its trajectory or time taken by the projectile to hit the ground is called time of flight.
Consider the example of a tower and projectile. Let h be the height of a tower. Let T be the time taken by the projectile to hit the ground, after being thrown horizontally from the tower.
We know that s y = uyt + 1/2 at2 for vertical motion. Here sy = h, t = T, uy = 0 (i.e., no initial vertical velocity). Then
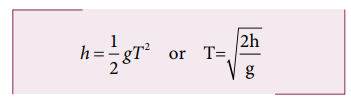
Thus, the time of flight for projectile motion depends on the height of the tower, but is independent of the horizontal velocity of projection. If one ball falls vertically and another ball is projected horizontally with some velocity, both the balls will reach the bottom at the same time. This is illustrated in the Figure 2.40.

(2) Horizontal range: The horizontal distance covered by the projectile from the foot of the tower to the point where the projectile hits the ground is called horizontal range. For horizontal motion, we have
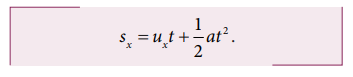
Here, sx = R (range), ux = u, a = 0 (no horizontal acceleration) T is time of flight. Then horizontal range = uT.
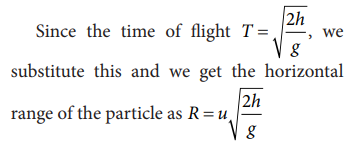
The above equation implies that the range R is directly proportional to the initial velocity u and inversely proportional to acceleration due to gravity g.
(3) Resultant Velocity (Velocity of projectile at any time): At any instant t, the projectile has velocity components along both x-axis and y-axis. The resultant of these two components gives the velocity of the projectile at that instant t, as shown in Figure 2.41.
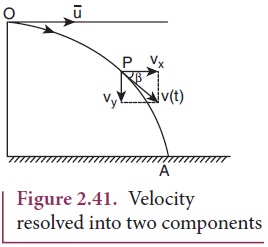
The velocity component at any t along horizontal (x-axis) is vx = ux + a x t
Since, ux = u, ax = 0 , we get
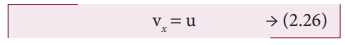
The component of velocity along vertical direction (y-axis) is v y = uy + a y t
Since, uy = 0, ay = g, we get
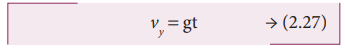
Hence the velocity of the particle at any instant is
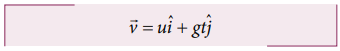
The speed of the particle at any instant t is given by
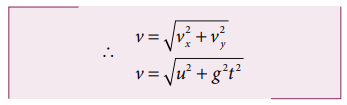
(4) Speed of the projectile when it hits the ground: When the projectile hits the ground after initially thrown horizontally from the top of tower of height h, the time of flight is
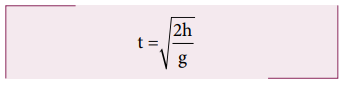
The horizontal component velocity of the projectile remains the same i.e vx= u
The vertical component velocity of the projectile at time T is
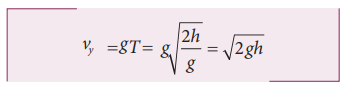
The speed of the particle when it reaches the ground is
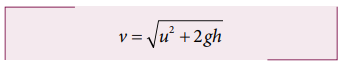
Solved Example Problems for Projectile Motion
Example 2.37
Suppose an object is thrown with initial speed 10 m s-1 at an angle π/4 with the horizontal, what is the range covered? Suppose the same object is thrown similarly in the Moon, will there be any change in the range? If yes, what is the change? (The acceleration due to gravity in the Moon gmoon = 1/6 g)
Solution
In projectile motion, the range of particle is given by,

If the same object is thrown in the Moon, the range will increase because in the Moon, the acceleration due to gravity is smaller than g on Earth,

The range attained on the Moon is approximately six times that on Earth.
Example 2.38
In the cricket game, a batsman strikes the ball such that it moves with the speed 30 m s-1 at an angle 30o with the horizontal as shown in the figure. The boundary line of the cricket ground is located at a distance of 75 m from the batsman? Will the ball go for a six? (Neglect the air resistance and take acceleration due to gravity g = 10 m s-2).
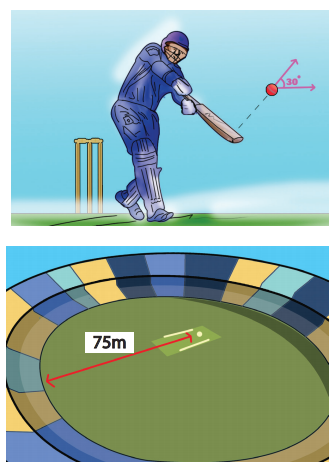
Solution
The motion of the cricket ball in air is essentially a projectile motion. As we have already seen, the range (horizontal distance) of the projectile motion is given by
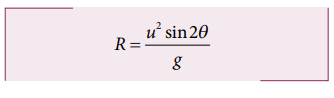
The initial speed u ![]() 30 m s-1
30 m s-1
The projection angle θ = 30o
The horizontal distance travelled by the cricket ball
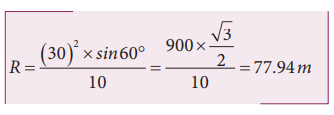
This distance is greater than the distance of the boundary line. Hence the ball will cross this line and go for a six.
Related Topics